
 上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.



 的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
 上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______;
上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为______; 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
 23、某研究性学习小组,为了了解某校七年级学生一天中做家庭作业所用的大致时间(时间以整数记.单位:分),对本校的初一学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图),请结合统计图中提供的信息,回答下列问题.
23、某研究性学习小组,为了了解某校七年级学生一天中做家庭作业所用的大致时间(时间以整数记.单位:分),对本校的初一学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图),请结合统计图中提供的信息,回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:
 14、某研究性学习小组,为了了解本校八年级学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本年级同学做了抽样调查,并整理绘制成直方图如图所示.
14、某研究性学习小组,为了了解本校八年级学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本年级同学做了抽样调查,并整理绘制成直方图如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
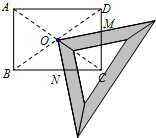 某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于| 44 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com