
| ����ʱ�� | �������� | �������� | |
| A���ͺ� | B���ͺ� | ||
| ��һ�� | 3̨ | 5̨ | 1800Ԫ |
| �ڶ��� | 4̨ | 10̨ | 3100Ԫ |
���� ��1������A��B�����ͺŵ�̨�Ƶļ۸��ͼ�������ݵó���ʽ��ʽ������ɣ�
��2�������̳����ò�����5400Ԫ�Ľ����������ͺŵ�̨�ƹ�30̨�������ó�����ʽ������ɣ�
��3������������Ϊ1400Ԫ�������ó���ʽ������ɣ�
��� �⣺��1����A��B�����ͺ�̨�Ƶ����۵��۷ֱ�ΪxԪ��yԪ��������ã�
$\left\{\begin{array}{l}{\left\{\begin{array}{l}{3x+5y=1800}\\{4x+10y=3100}\end{array}\right.}\\{\;}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=250}\\{y=210}\end{array}\right.$
��A��B�����ͺ�̨�Ƶ����۵��۷ֱ�Ϊ250Ԫ��210Ԫ��
��2����ɹ�A���ͺ�̨��ą����ɹ�B���ͺ�̨�ƣ�30-a��̨��
������ã�200a+170��30-a����5400��
��ã�a��10��
�𣺳������ɹ�A���ͺ�̨��10̨ʱ���ɹ�������5400Ԫ��
��3������������250-200��a+��210-170����30-a��=1400��
��ã�a=20����ʱ��a��10��
�����ڣ�2���������³��в���ʵ������1400Ԫ��Ŀ�꣬
���� ������Ҫ�����˶�Ԫһ�η������Ӧ���Լ�һԪһ�η��̵�Ӧ�ú�һԪһ�β���ʽ��Ӧ�õ�֪ʶ����������ó���ȷ�ĵ�����ϵ�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3��-3�� | B�� | ��-2��3�� | C�� | ��1��6�� | D�� | ��-2��-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һö������ֱ����1��6����ľ������������ӣ�����һ��ĵ����ǡ�5�� | |
| B�� | ����ѡ��ij������Ƶ�������ڲ��Ŷ���Ƭ | |
| C�� | ��ƽ���ڣ�����һ�������ε��ڽǶ��������Ϊ360�� | |
| D�� | �����ݻ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3•a2=a6 | B�� | a6��a3=a2 | C�� | ��a2��3=a6 | D�� | a2+a2=2a4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2015 | B�� | -2015 | C�� | $\frac{1}{2015}$ | D�� | -$\frac{1}{2015}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
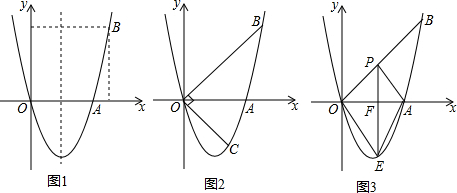
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com