
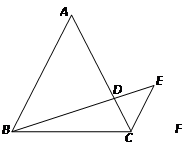
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
1.求证:△ABD∽△CED.
2.若AB=6,AD=2CD,求BE的长.
1.证明:∵ △ABC是等边三角形,
∴ ∠BAC=∠ACB=60°.∠ACF=120°.
∵ CE是外角平分线, ∴ ∠ACE=60°.
∴ ∠BAC=∠ACE。
又∵ ∠ADB=∠CDE,
∴ △ABD∽△CED。
2.解:作BM⊥AC于点M,AC=AB=6.
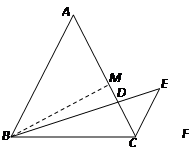
∴ AM=CM=3,BM=AB·sin60°=![]() .
.
∵ AD=2CD,∴ CD=2,AD=4,MD=1。
在Rt△BDM中,BD=![]() =
=![]() .
.
由(1)△ABD∽△CED得,![]() ,
,![]() ,
,
∴ ED=![]() ,∴ BE=BD+ED=
,∴ BE=BD+ED=![]() 。
。
解析:(1)由于△ABC是等边三角形,易知∠A=60°,∠ACF=120°;而CE平分∠ACF,可得∠A=∠DCE=60°,又已知了一组对顶角,两组对应角相等,可判定所求的两个三角形相似;
(2)由于△ABC是等边三角形,则AC=BC=6,由此可求出AC、CD的长;过B作BM⊥AC于M,根据等边三角形的性质知AM=MC,由此可求出MD、MB的长,进而可由勾股定理求出BD的长;根据(1)的相似三角形,可得出关于AD、CD,BD、DE的比例关系式,即可求出DE的长,从而由BE=BD+DE求出BE的长.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
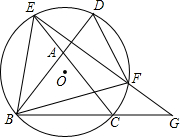 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com