练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若﹣x3ya与xby是同类项，则a+b的值为（ ）
    A.2
    B.3
    C.4
    D.5

    【答案】C
    【解析】解：∵﹣x3ya与xby是同类项，
    ∴a=1，b=3，
    则a+b=1+3=4．
    故选C．
    根据同类项中相同字母的指数相同的概念求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】解方程（组）：
    （1）
    （2）解二元一次方程组 有位同学是这么做的，①+②得4x=20，解得x=5，代入①得y=﹣3．
    ∴这个方程组的解为 ．
    该同学解这个二元一次方程组的过程中使用了消元法，目的是把二元一次方程组转化为求解；
    （3）请你换一种方法来求解（2）中二元一次方程组．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E，F分别在边BC和CD上，下列结论：①CE=CF= ；②∠BAE=15°；③BE+DF=EF；④S正方形ABCD=2+ ．其中正确的序号是（把你认为正确的都填上）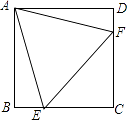

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2018年中国与“一带一路”沿线国家进出口总额约13000 0000 0000美元，用科学记数法表示这个进出口总额为_____美元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（﹣2）2n+1+2（﹣2）2n＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知x=2是关于x的方程3x+a=0的一个解，则a的值是（ ）
    A.﹣6
    B.﹣3
    C.﹣4
    D.﹣5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．

    （1）画出△ABC向上平移6个单位得到的△A1B1C1；

    （2）以点C为位似中心，在网格中画出△A2B2C2，使△A2B2C2与△ABC位似，且△A2B2C2与△ABC的位似比为2：1，并直接写出点A2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】去年冬季的某一天，学校一室内温度是8℃，室外温度是﹣2℃，则室内外温度相差℃．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在菱形ABCD中，AC=2，BD=2，AC，BD相交于点O．
    （1）求边AB的长；
    （2）如图2，将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别与边BC，CD相交于点E，F，连接EF与AC相交于点G．
    ①判断△AEF是哪一种特殊三角形，并说明理由；
    ②旋转过程中，当点E为边BC的四等分点时（BE＞CE），求CG的长．

    查看答案和解析>>

    同步练习册答案