练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】anbn+1·(abn)3________________

    【答案】an+3b4n+1

    【解析】

    原式先根据积的乘方法则进行计算，再根据同底数幂的乘法法则进行计算即可．

    解：anbn+1·(abn)3= anbn+1·a3b3n=an+3bn+1+3n=an+3b4n+1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，一次函数y＝k1x＋b的图象与x轴交于点A（－3，0），与y轴交于点B，且与正比例函数y＝kx的图象交点为C（3，4）．

    （1）求正比例函数与一次函数的关系式；

    （2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，请求出点D的坐标；

    （3）在x轴上是否存在一点E使△BCE周长最小，若存在，求出点E的坐标

    （4）在x轴上求一点P使△POC为等腰三角形，请直接写出所有符合条件的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC，△ABC的高CD与角平分线AE相交点F，过点C作CH⊥AE于G，交AB于H．

    （1）求∠BCH的度数；

    （2）求证：CE＝BH．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ABC与∠ACB的平分线相交于点O．过点O作EF∥BC．分别交AB和AC于点E、F.

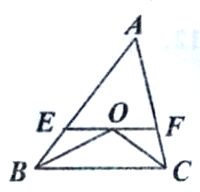
    (l)你能发现哪些结论，把它们写出来．并选择一个加以证明；

    (2)若AB=10，AC=8．试求△AFF的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图8，四边形ABEG、GEFH、HFCD都是边长为1的正方形.

    （1）求证：△AEF∽△CEA；

    （2）求证：∠AFB+∠ACB=45°.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于命题“如果∠1+∠2=90°，那么∠1≠∠2”，能说明它是假命题的反例是（　　）

    A. ∠1=60°，2=40° B. ∠1=50°，∠2=40°

    C. ∠1=∠2=40° D. ∠1=∠2=45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连接BD，CE，BD和CE相交于点F，若△ABC不动，将△ADE绕点A任意旋转一个角度．

    （1）求证：△BAD≌△CAE．

    （2）如图①，若∠BAC=∠DAE=90°，判断线段BD与CE的关系，并说明理由；

    （3）如图②，若∠BAC=∠DAE=60°，求∠BFC的度数；

    （4）如图③，若∠BAC=∠DAE= ，直接写出∠BFC的度数（不需说明理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知三角形的两边a＝3，b＝7，则下列长度的四条线段中能作为第三边c的是（　　）
    A.3
    B.4
    C.7
    D.10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用不等式表示:“2与x的和的3倍是负数”为_________________.

    查看答案和解析>>

    同步练习册答案