
【题目】如图,△ABC中,∠ABC与∠ACB的平分线相交于点O.过点O作EF∥BC.分别交AB和AC于点E、F.
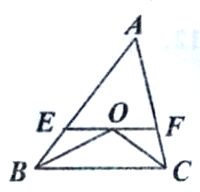
(l)你能发现哪些结论,把它们写出来.并选择一个加以证明;
(2)若AB=10,AC=8.试求△AFF的周长.
【答案】(1)见解析;(2)18
【解析】试题分析:
(1)结合图形和已知条件分析易得:①OE=BE;②OF=CF;③EF=BE+CF;
(2)由第一问中的结论③EF=BE+CF结合AB=10,AC=8易得△AEF的周长为:AB+AC=18.
试题解析:
(1)由已知可推得的结论有:①OE=BE;②OF=FC;③EF=BE+CF;
现将结论③证明如下:
∵BO平分∠ABC,
∴∠EBO=∠OBC.
∵EF∥BC,
∴∠EOB=∠OBC,
∴∠EBO=∠EOB,
∴OE=BE.
同理可得:OF=CF.
∴EF=OE+OF=BE+CF.
(2)由(1)可得:EF=BE+CF,又∵AB=10,AC=8,
∴ △AEF的周长=AE+EF+AF=AE+BE+AF+CF=AB+AC=10+8=18.


科目:初中数学 来源: 题型:
【题目】某市户籍人口1694000人,则该市户籍人口数据用科学记数法可表示为( )
A.1.694×104人
B.1.694×105人
C.1.694×106人
D.1.694×107人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
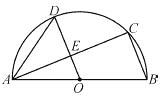
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
, ![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过坐标原点
经过坐标原点![]() ,与抛物线的一个交点为
,与抛物线的一个交点为![]() ,与抛物线的对称交于点
,与抛物线的对称交于点![]() ,连接
,连接![]() ,点
,点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() .
.
(![]() )求抛物线的解析式,并分别求出点
)求抛物线的解析式,并分别求出点![]() 和点
和点![]() 的坐标.
的坐标.
(![]() )在抛物线上是否存在点
)在抛物线上是否存在点![]() ,使
,使![]() ≌
≌![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
(![]() )如图①,点
)如图①,点![]() 和点
和点![]() 均在⊙
均在⊙![]() 上,且
上,且![]() ,点
,点![]() 和点
和点![]() 均在射线
均在射线![]() 上,若
上,若![]() ,则点
,则点![]() 与⊙
与⊙![]() 的位置关系是__________;若
的位置关系是__________;若![]() ,则点
,则点![]() 与⊙
与⊙![]() 的位置关系是__________.
的位置关系是__________.
问题解决:
如图②,图③所示,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,点
,点![]() 是
是![]() 边上任意一点.
边上任意一点.
(![]() )当
)当![]() 时,求
时,求![]() 的长度.
的长度.
(![]() )是否存在点
)是否存在点![]() ,使得
,使得![]() 最大?若存在,请说明理由,并求出
最大?若存在,请说明理由,并求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是 ( )

A. 56° B. 60° C. 68° D. 94°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为_____.
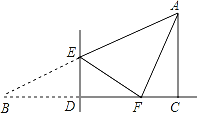
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com