
【题目】问题发现:
(![]() )如图①,点
)如图①,点![]() 和点
和点![]() 均在⊙
均在⊙![]() 上,且
上,且![]() ,点
,点![]() 和点
和点![]() 均在射线
均在射线![]() 上,若
上,若![]() ,则点
,则点![]() 与⊙
与⊙![]() 的位置关系是__________;若
的位置关系是__________;若![]() ,则点
,则点![]() 与⊙
与⊙![]() 的位置关系是__________.
的位置关系是__________.
问题解决:
如图②,图③所示,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,点
,点![]() 是
是![]() 边上任意一点.
边上任意一点.
(![]() )当
)当![]() 时,求
时,求![]() 的长度.
的长度.
(![]() )是否存在点
)是否存在点![]() ,使得
,使得![]() 最大?若存在,请说明理由,并求出
最大?若存在,请说明理由,并求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.



【答案】(![]() )点
)点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 外;(
外;(![]() )
)![]() 或
或![]() ;(
;(![]() )当
)当![]() 有最大值时,
有最大值时, ![]() 长为
长为![]() .
.
【解析】试题分析:(1)根据题意得:点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 外;
外;
(2)以AD为斜边等腰直角三角形AOD ,以点O为圆心,OA为半径作⊙O交BC于点E.在RtΔAOD中可计算OA=2,连接OP,则OP=PA=2,过点![]() 作
作![]() 于点
于点![]() ,可求出BO=2,再进而求出BC的值,确定点P的个数;
,可求出BO=2,再进而求出BC的值,确定点P的个数;
(3)存在.
试题解析:(1)点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 外;
外;
(![]() )以
)以![]() 为斜边等腰直角三角形
为斜边等腰直角三角形![]() ,
,
以点![]() 为圆心,
为圆心, ![]() 为半径作⊙
为半径作⊙![]() 交
交![]() 于点
于点![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴ ![]() ,
,
连接![]() ,则
,则![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
, ![]() ,∴
,∴ ![]() .
.
又∵![]() ,∴四边形
,∴四边形![]() 为矩形,
为矩形,
∴![]() ,
, ![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() .
.
又∵经计算![]() ,
,
∴符合条件的点![]() 有
有![]() 个.
个.
![]() 的长为
的长为![]() 或
或![]() .
.
(![]() )存在,作
)存在,作![]() 的中垂线,交
的中垂线,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,在
,在![]() 上取点
上取点![]() ,
,
以![]() 为半径作⊙
为半径作⊙![]() ,当⊙
,当⊙![]() 与
与![]() 相切于点
相切于点![]() 时,
时, ![]() 最大.
最大.
理由:在![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,
, ![]() 交⊙
交⊙![]() 于
于![]() ,连接
,连接![]() ,
,
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
连接![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .
.
∵![]() ,
, ![]() ,∴
,∴ ![]() ,
,
∴![]() 和
和![]() 均为等腰直角三角形.
均为等腰直角三角形.
∴![]() ,
, ![]() ,
, ![]() .
.
∵![]() ,
, ![]() ,
,
∵⊙![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,∴
,∴ ![]() ,
,
又∵![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∴设![]() ,则
,则![]() ,
, ![]()
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
解得: ![]() (舍),
(舍),![]() ,
,
∴![]() ,
,
∴当![]() 有最大值时,
有最大值时, ![]() 长为
长为![]() .
.


科目:初中数学 来源: 题型:
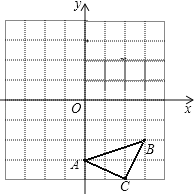
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC与∠ACB的平分线相交于点O.过点O作EF∥BC.分别交AB和AC于点E、F.
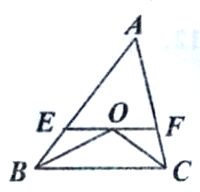
(l)你能发现哪些结论,把它们写出来.并选择一个加以证明;
(2)若AB=10,AC=8.试求△AFF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC⊥AB,DB⊥AB,AC=BE,CE=DE,
(1)证明:△ACE≌△BED;
(2)试猜想线段CE与DE位置关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是( )
A. ∠1=60°,2=40° B. ∠1=50°,∠2=40°
C. ∠1=∠2=40° D. ∠1=∠2=45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com