
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
, ![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过坐标原点
经过坐标原点![]() ,与抛物线的一个交点为
,与抛物线的一个交点为![]() ,与抛物线的对称交于点
,与抛物线的对称交于点![]() ,连接
,连接![]() ,点
,点![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() .
.
(![]() )求抛物线的解析式,并分别求出点
)求抛物线的解析式,并分别求出点![]() 和点
和点![]() 的坐标.
的坐标.
(![]() )在抛物线上是否存在点
)在抛物线上是否存在点![]() ,使
,使![]() ≌
≌![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ,
, ![]() ,
, ![]() ;(2)
;(2)![]() 或
或![]()
【解析】试题分析:(1)利用待定系数法求抛物线的函数表达式和直线DE的解析式,利用配方法求抛物线的对称轴,即点E的横坐标为x=3,代入直线DE中可求得E的纵坐标,根据对称性求得点B的坐标;
(2)如图,根据△FOE≌△FCE,对应边相等,得FC=FO,所以F在OC的中垂线上,点F纵坐标为-4,代入抛物线后求得点F的坐标
试题解析:(![]() )∵抛物线
)∵抛物线![]() 经过点
经过点![]() ,
, ![]() ,
,
∴![]() ,计算得出
,计算得出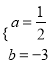 ,
,
∴抛物线的函数表达式![]() ,
,
∵![]() ,
,
∴抛物线的对称轴为直线![]() .
.
又抛物线与![]() 轴交于
轴交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .
.
∴点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的函数表达式为
的函数表达式为![]() .
.
∵点![]() ,计算得出
,计算得出![]() ,
,
∴直线![]() 的函数表达式为
的函数表达式为![]() ,
,
∵点![]() 为直线
为直线![]() 和抛物线对称轴的交点,
和抛物线对称轴的交点,
∴点![]() 的横坐标为
的横坐标为![]() ,纵坐标不
,纵坐标不![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
(![]() )抛物线上存在点
)抛物线上存在点![]() ,使
,使![]() ≌
≌![]() .
.
∵![]() ,
,
∴![]() ,
,
∴点![]() 在
在![]() 的垂直平分线上,此时点
的垂直平分线上,此时点![]() 的纵坐标为
的纵坐标为![]() .
.
∴![]() ,计算得出
,计算得出![]() ,
,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=3,BC=4,D是AB上一动点(不与A、B重合),DE⊥AC于点E,DF⊥BC于点F,点D由A向B移动时,矩形DECF的周长变化情况是( )

A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.
(1)求∠BCH的度数;
(2)求证:CE=BH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了追求更合适的出行体验,利用网络呼叫专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用![]() (元)与行驶里程
(元)与行驶里程![]()
![]() 的函数关系如图所示,请根据图象解答下列问题:
的函数关系如图所示,请根据图象解答下列问题:
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )若专车低还行驶(时速
)若专车低还行驶(时速![]() ),每分钟另加
),每分钟另加![]() 元的低速费(不足
元的低速费(不足![]() 分钟的部分按
分钟的部分按![]() 分钟计算).某乘客有一次在非高峰期乘坐专车,途中低速行驶了
分钟计算).某乘客有一次在非高峰期乘坐专车,途中低速行驶了![]() 分钟,共付费
分钟,共付费![]() 元,求这位乘客坐专车的行驶里程.
元,求这位乘客坐专车的行驶里程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC与∠ACB的平分线相交于点O.过点O作EF∥BC.分别交AB和AC于点E、F.
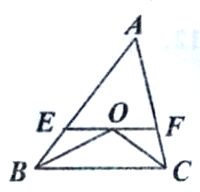
(l)你能发现哪些结论,把它们写出来.并选择一个加以证明;
(2)若AB=10,AC=8.试求△AFF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,四边形ABEG、GEFH、HFCD都是边长为1的正方形.
(1)求证:△AEF∽△CEA;
(2)求证:∠AFB+∠ACB=45°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,连接BD,CE,BD和CE相交于点F,若△ABC不动,将△ADE绕点A任意旋转一个角度.
(1)求证:△BAD≌△CAE.
(2)如图①,若∠BAC=∠DAE=90°,判断线段BD与CE的关系,并说明理由;
(3)如图②,若∠BAC=∠DAE=60°,求∠BFC的度数;
(4)如图③,若∠BAC=∠DAE= ![]() ,直接写出∠BFC的度数(不需说明理由)
,直接写出∠BFC的度数(不需说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于![]() CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
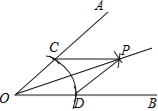
A. SAS B. ASA C. AAS D. SSS
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com