
【题目】如图,反比例函数y= ![]() 的图象经过A、B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为1,则k的值为 .
的图象经过A、B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为1,则k的值为 . 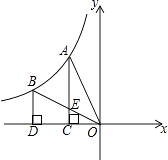
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE.若SΔABC=18,△ADF的面积为![]() ,△CFE的面积为
,△CFE的面积为![]() ,则
,则![]()
![]() =________
=________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明今年五一节去三峡广场逛水果超市,他分两次购进了![]() 、
、![]() 两种不同单价的水果.第一次购买
两种不同单价的水果.第一次购买![]() 种水果的数量比
种水果的数量比![]() 种水果的数量多50%,第二次购买
种水果的数量多50%,第二次购买![]() 种水果的数量比第一次购买
种水果的数量比第一次购买![]() 种水果的数量少60%,结果第二次购买水果的总数量比第一次购买水果的总数量多20%,且第二次购买
种水果的数量少60%,结果第二次购买水果的总数量比第一次购买水果的总数量多20%,且第二次购买![]() 、
、![]() 水果的总费用比第一次购买
水果的总费用比第一次购买![]() 、
、![]() 水果的总费用少10%(两次购买中
水果的总费用少10%(两次购买中![]() 、
、![]() 两种水果的单价不变),则
两种水果的单价不变),则![]() 种水果的单价与
种水果的单价与![]() 种水果的单价的比值是______.
种水果的单价的比值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数![]() 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题: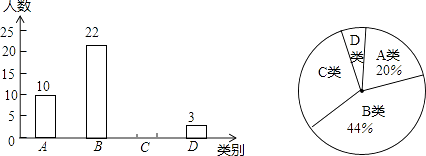
(1)本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分 | 0 | 2 | 4 | 6 | 8 | 10 |
h/厘米 | 30 | 29 | 28 | 27 | 26 | 25 |
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式_____;这根蜡烛最多能燃烧的时间为_____分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两点在直线m上,C,D两点在直线n上,∠BAD=α,∠BCD=β.
(1)如图1,若∠BAD=∠ADC,求证∠ABC=∠BCD.
(2)如图2,m∥n,过点D作DE⊥BC于点E,∠BAD与∠DEB的角平分线相交于点P,求∠P(用α,β的式子表示)
(3)在(2)的条件下,若点A沿直线m向右运动,且不与B点重合,则∠APE= (用α,β的式子表示,不写证明过程).


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com