
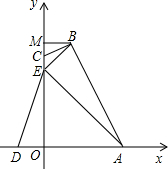
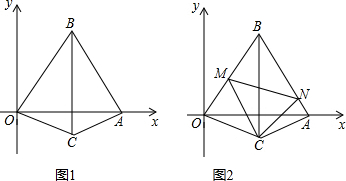
 ��ͼ���ı���OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ�����B��BM��y�ڵ�M��OE=OA=3��OD=1������AE��BE��DE����֪tan��CBE=$\frac{1}{3}$��B��1��4����
��ͼ���ı���OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ�����B��BM��y�ڵ�M��OE=OA=3��OD=1������AE��BE��DE����֪tan��CBE=$\frac{1}{3}$��B��1��4�������� ��1�����ݵ�B������õ�MB=1��OM=4������OA=OC���õ���OAE=��OEA=45�㣬��Rt��EMB�У�EM=OM-OE=1=BM�����ԡ�MEB=��MBE=45�㣬�õ���OAE=��MBE=45�㣬��OEA=��MEB=45�㣬�Ӷ��õ���AEO����BEM��
��2���ɣ�1��֪����OEA+��MEB=90�㣬�����BEA=180��-��OEA-��MEB=90�㣬�õ�AB�ǡ�ABE���Բ��ֱ����ͨ�����ɶ������BE��AE���ɴ����tan��BAE=$\frac{BE}{AE}$=$\frac{\sqrt{2}}{3\sqrt{2}}=\frac{1}{3}$����tan��CBE=$\frac{1}{3}$�����ԡ�BAE=��CBE����á�CBA=90�㣬��CB��AB������CB�ǡ�ABE���Բ�����ߣ�
��3����ֱ��AB�Ľ���ʽΪy=kx+b����A��3��0����B��1��4������y=kx+b�����y=-2x+6������E������EF��x�ύAB�ڵ�F�������F��$\frac{3}{2}$��3��������������������ۣ�
���һ����ͼ2����0��t��$\frac{3}{2}$ʱ�����AOEƽ�Ƶ���PNM��λ�ã�MD��AB�ڵ�H��MN��AE�ڵ�G����ON=AP=t������H��LK��x���ڵ�K����EF�ڵ�L�����á�AHP�ס�FHM����FHL�ס�AHK�����HK=2t�����ԡ�AOE���ABE�ص����ֵ����S=S��MNP-S��GNA-S��HAP��
���������ͼ3����$\frac{3}{2}$��t��3ʱ�����AOEƽ�Ƶ���PQR��λ�ã�PQ��AB�ڵ�I����AE�ڵ�V�����á�IQA�ס�IPF�����IQ=2��3-t�����ԣ���AOE���ABE�ص����ֵ����S=S��IQA-S��VQA��
��� �⣺��1��֤������ͼ1��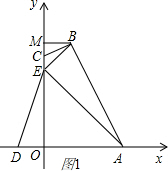
�ߵ�B�������ǣ�1��4����
��MB=1��OM=4��
��Rt��AOE��OA=OE=3��
���OAE=��OEA=45�㣮
��Rt��EMB��EM=OM-OE=1=BM��
���MEB=��MBE=45�㣮
���OAE=��MBE=45�㣮
��OEA=��MEB=45�㣬
���AEO����BEM��
��2���ɣ�1��֪����OEA+��MEB=90��
���BEA=180��-��OEA-��MEB=90�㣮
��AB�ǡ�ABE���Բ��ֱ����
��Rt��AOE��OA=OE=3��AE=$\sqrt{O{A}^{2}+O{E}^{2}}=3\sqrt{2}$��
��Rt��EMB��EM=BM=1��BE=$\sqrt{E{M}^{2}+B{M}^{2}}=\sqrt{2}$��
��Rt��ABE��tan��BAE=$\frac{BE}{AE}$=$\frac{\sqrt{2}}{3\sqrt{2}}=\frac{1}{3}$��
��tan��CBE=$\frac{1}{3}$��
���BAE=��CBE��
��Rt��ABE�У���BAE+��ABE=90�㣬
���CBE+��ABE=90�㣬
���CBA=90�㣬
��CB��AB��
��CB�ǡ�ABE���Բ�����ߣ�
��3���⣺��ֱ��AB�Ľ���ʽΪy=kx+b��
��A��3��0����B��1��4�����룬�ã�$\left\{\begin{array}{l}{3k+b=0}\\{k+b=4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$��
��y=-2x+6��
����E������EF��x�ύAB�ڵ�F��
��y=3ʱ����x=$\frac{3}{2}$��
��F��$\frac{3}{2}$��3����
���һ����ͼ2����0��t��$\frac{3}{2}$ʱ�����AOEƽ�Ƶ���PNM��λ�ã�MD��AB�ڵ�H��MN��AE�ڵ�G��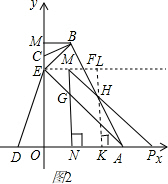
��ON=AD=t������H��LK��x���ڵ�K����EF�ڵ�L��
��EF��x�ᣬ
���AHP�ס�FHM����FHL�ס�AHK��
��$\frac{AP}{FM}=\frac{AH}{FH}��\frac{AH}{FH}=\frac{HK}{HL}$��
��$\frac{AP}{FM}=\frac{HK}{HL}$����$\frac{t}{\frac{3}{2}-t}=\frac{HK}{3-HK}$��
��ã�HK=2t��
���AOE���ABE�ص����ֵ����S=S��MNP-S��GNA-S��HAP=$\frac{1}{2}$��3��3-$\frac{1}{2}��$��3-t��2-$\frac{1}{2}$t•2t=-$\frac{3}{2}$t2+3t��
���������ͼ3����$\frac{3}{2}$��t��3ʱ�����AOEƽ�Ƶ���PQR��λ�ã�PQ��AB�ڵ�I����AE�ڵ�V��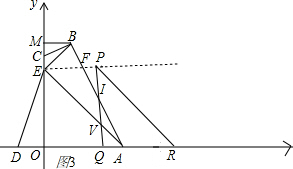
��EF��x�ᣬ
���IQA�ס�IPF��
��$\frac{AQ}{FP}=\frac{IQ}{IP}$��
��$\frac{3-t}{t-\frac{3}{2}}=\frac{IQ}{3-IQ}$��
��ã�IQ=2��3-t����
���AOE���ABE�ص����ֵ����S=S��IQA-S��VQA=$\frac{1}{2}$����3-t����2��3-t��-$\frac{1}{2}$��3-t��2=$\frac{1}{2}$��3-t��2=$\frac{1}{2}$t2-3t+$\frac{9}{2}$��
����������s=$\left\{\begin{array}{l}{-\frac{3}{2}{t}^{2}+3t��0��t��\frac{3}{2}��}\\{\frac{1}{2}{t}^{2}-3t+\frac{9}{2}��\frac{3}{2}��t��3��}\end{array}\right.$��
���� ���⿼�������������ε��ж������ʡ�Բ�����ߵ��ж���������ϵʽ���������Ĺؼ����������߹������������ƣ��Լ����ν��˼���Ӧ�ã�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{20}$ | B�� | $\sqrt{19}$ | C�� | $\sqrt{18}$ | D�� | $\sqrt{\frac{1}{5}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У�������ABCD�Ķ���A����y���ϣ���C����x���ϣ����Ŷ���C��ԭ��O��x�������᷽���˶�������A��y�Ḻ���᷽���˶����յ�O�����˶�������OD�ij��ȱ仯����ǣ�������
��ͼ����ƽ��ֱ������ϵ�У�������ABCD�Ķ���A����y���ϣ���C����x���ϣ����Ŷ���C��ԭ��O��x�������᷽���˶�������A��y�Ḻ���᷽���˶����յ�O�����˶�������OD�ij��ȱ仯����ǣ�������| A�� | һֱ���� | B�� | һֱ��С | C�� | �ȼ�С������ | D�� | ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com