
| A. | $\sqrt{20}$ | B. | $\sqrt{19}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{5}}$ |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查定义中的两个条件(①被开方数不含分母;②被开方数不含能开得尽方的因数或因式)是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:A、$\sqrt{20}=2\sqrt{5}$,不是最简二次根式,错误;
B、符合最简二次根式的条件;故本选项正确;
C、$\sqrt{18}=3\sqrt{2}$,不是最简二次根式,错误;
D、$\sqrt{\frac{1}{5}}=\frac{\sqrt{5}}{5}$,不是最简二次根式,错误;
故选B
点评 本题主要考查了最简二次根式的定义,最简二次根式必须满足两个条件:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
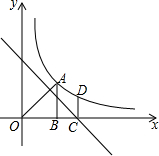 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2,2),过点A作AB⊥x轴,交x轴于点B,在x轴上有一点C,点C在点B的右侧,过点C作直线OA的垂线l,在反比例函数图象上有一点D,点B和点D关于直线l对称.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2,2),过点A作AB⊥x轴,交x轴于点B,在x轴上有一点C,点C在点B的右侧,过点C作直线OA的垂线l,在反比例函数图象上有一点D,点B和点D关于直线l对称.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
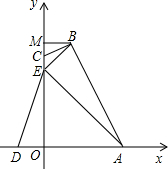 如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,过点B作BM⊥y于点M,OE=OA=3,OD=1,连接AE、BE、DE.已知tan∠CBE=$\frac{1}{3}$,B(1,4).
如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,过点B作BM⊥y于点M,OE=OA=3,OD=1,连接AE、BE、DE.已知tan∠CBE=$\frac{1}{3}$,B(1,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com