
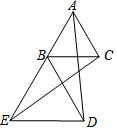
 如图所示,已知△ABC和△BDE均为等边三角形,连接AD、CE,若∠BAD=39°,那么∠ACE=99°.
如图所示,已知△ABC和△BDE均为等边三角形,连接AD、CE,若∠BAD=39°,那么∠ACE=99°. 分析 易证∠ABD=∠CBE,即可证明△ABD≌△CBE,可得∠AEC=∠ADB,即可解题.
解答 解:∵△ABC和△BDE均为等边三角形,
∴∠ABC=∠DBE=60°,AB=BC,BE=BD,
∴∠CBD=60°,
∴∠ABD=∠CBE=120°,
在△ABD和△CBE中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠CBE}\\{BE=BD}\end{array}\right.$,
∴△ABD≌△CBE,(SAS)
∴∠AEC=∠ADB,
∵∠ADB=180°-∠ABD-∠BAD=21°,
∴∠AEC=21°,
∴∠ACE=99°,
故答案为:99°.
点评 本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABD≌△CBE是解题的关键.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
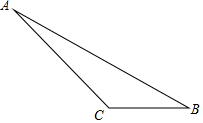 按下列要求作图并解答:
按下列要求作图并解答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1项 | B. | 2项 | C. | 3项 | D. | 4项 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同弧或等弧所对的圆周角相等 | B. | 平分弦的直径垂直于弦 | ||
| C. | 两条平行线间的距离处处相等 | D. | 直径所对的圆周角等于90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+2xy+4y2 | B. | 25m2+10mn+n2 | C. | a2+ab+b2 | D. | x2-2xy-$\frac{1}{4}$y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${({\frac{1}{3}})^5}$米 | B. | ${({\frac{2}{3}})^5}$米 | C. | $[{1-{{({\frac{1}{3}})}^5}}]$米 | D. | $[{1-{{({\frac{2}{3}})}^5}}]$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
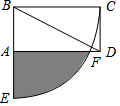 如图,已知矩形ABCD中,AB=1 cm,BC=2 cm,以B为圆心,BC为半径作$\frac{1}{4}$圆弧交AD于点F,交BA的延长线于点E,则扇形BCE被矩形所截剩余部分的面积为$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.
如图,已知矩形ABCD中,AB=1 cm,BC=2 cm,以B为圆心,BC为半径作$\frac{1}{4}$圆弧交AD于点F,交BA的延长线于点E,则扇形BCE被矩形所截剩余部分的面积为$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com