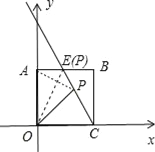
【题目】如图，已知点C（4，0）是正方形AOCB的一个顶点，直线PC交AB于点E，若E是AB的中点.

（1）求点E的坐标；

（2）求直线PC的解析式；

（3）若点P是直线PC在第一象限的一个动点，当点P运动到什么位置时，图中存在与△AOP全等的三角形？请求出P点的坐标，并说明理由.

参考答案：

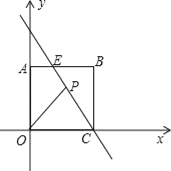
【答案】（1）点E的坐标为（2，4）；（2）直线PC的解析式为y=﹣2x+8；（3）点P坐标为（2，4）或（， ）.

【解析】试题分析：（1）因为E是AB中点，计算出A和B的坐标即可算出E的坐标；
（2）根据E和C的坐标即可求出直线PC的解析式；
（3）根据全等三角形的判定方法，找出全部的点P即可．

试题解析：（1）∵四边形AOCB是正方形，C（4，0），∴点B（4，4），C（4，0），

∵E是AB的中点，∴点E的坐标为（2，4）.

（2）设直线PC的解析式为y=kx+b，将点E（2，4）、C（4，0）代入y=kx+b中，

得： ，解得： ，

∴直线PC的解析式为y=﹣2x+8.

（3）有两种情况，如图所示.

①当点P与点E重合时，

在△OAE和△CBE中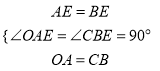， ，∴△OAE≌△CBE（SAS），

此时点P坐标为（2，4）；

②当AP等于CP时，

在△AOP和△COP中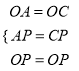， ，∴△AOP≌△COP（SSS），∴∠AOP=∠COP=45°，

∴直线OP的解析式为y=x.

联立直线OP、PC的解析式得： ，解得： ，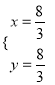

∴此时点P的坐标为（， ）.

关闭