
| 价格 类型 | 进价(元/件) | 售价(元/件) |
| A | 30 | 45 |
| 售价(元/部) | 50 | 70 |
分析 (1)设商场应购进A种服装x件,表示出B种服装(100-x)件,然后根据进货款=A种服装的进货款+B种服装的进货款列出方程求解即可;
(2)根据“商场规定B种服装进货数量不超过A种服装进货数量的三倍,且超过A种服装进货数量的2倍”,列出不等式组,求出x的范围,即可解答;
(3)设商场销售完这批服装可获利y元,根据获利等于两种服装的获利总和列式整理,再根据x的取值范围,然后根据一次函数的增减性求出获利的最大.
解答 解:(1)设商场应购进A种服装x件,则B种服装(100-x)件,根据题意得:
30x+50(100-x)=3500,
解得x=75,
所以100-x=100-75=25.
答:应购进A种服装75件,则B种服装25件;
(2)设商场应购进A种服装x件,则B种服装(100-x)件,
根据题意得:
$\left\{\begin{array}{l}{100-x≤3x}\\{100-x>2x}\end{array}\right.$
解得:$25≤x<33\frac{1}{3}$,
∵x为正整数,
∴x=25,26,27,28,29,30,31,32,33,
有9种进货方案:
①A种服装25件,B种服装75件;②A种服装26件,B种服装74件;③A种服装27件,B种服装73件;④A种服装28件,B种服装72件;⑤A种服装29件,B种服装71件;⑥A种服装30件,B种服装70件;⑦A种服装31件,B种服装69件;⑧A种服装32件,B种服装68件;⑨A种服装33件,B种服装67件;
(3)设商场销售完这批服装可获利y元,
则y=(45-30)x+(70-50)(100-x),
=15x+2000-20x,
=-5x+2000,
即y=-5x+2000,
∵k=-5<0,
∴y随x的增大而减小,
∵$25≤x<33\frac{1}{3}$,
∴x=25时,y取得最大值,为-5×25+2000=1875(元).
答:商场购进A种服装75件,B种服装25件销售完这批服装时获利最多,此时利润为1875元.
点评 本题考查了一次函数的应用,主要利用了一次函数的增减性,(2)题中理清题目数量关系并列式求出x的取值范围是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
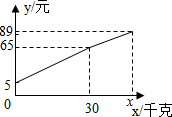 一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题:
一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
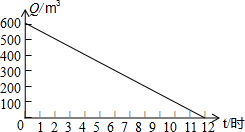 河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是200米3.
河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是200米3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
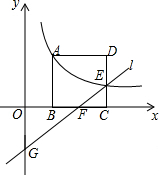 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{4}$,0).
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{4}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
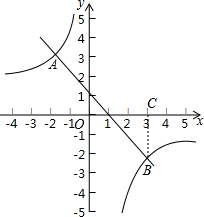 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(-2,3),B(3,n)两点.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(-2,3),B(3,n)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com