
【题目】如图1,在△ABC中,AE⊥BC于点E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由.

【答案】(1)BD⊥AC,BD=AC(2)BD⊥AC,BD=AC
【解析】试题分析:
(1)延长BD交AC于点F,用SAS证明△BDE≌△ACE即可解题;
(2)用SAS证明△BDE≌△ACE可得BD=AC,再证∠AFB=90°即可.
(1)BD⊥AC,BD=AC.
试题解析:
证明:延长BD交AC于点F. ∵AE⊥BC于点E, ∴∠BED=∠AEC=90°.又AE=BE,DE=CE, ∴△DBE≌△CAE(SAS). ∴BD=AC, ∠DBE=∠CAE,∠BDE=∠ACE. ∵∠BDE=∠ADF, ∴ ∠ADF=∠ACE. ∵∠ACE+∠CAE=90°, ∴∠ADF+∠CAE=90°. ∴BD⊥AC.
(2)BD⊥AC,BD=AC.
证明: ∵∠AEB=∠DEC=90°, ∴∠AEB+∠AED=∠DEC+∠AED,即∠BED=∠AEC.又AE=BE,DE=CE, ∴△DBE≌△CAE(SAS). ∴BD=AC, ∠DBE=∠CAE,∠BDE=∠ACE. ∵∠BFC=∠ACD+∠CDE +∠BDE=∠ACD+∠CDE +∠ACE=∠ECD+∠CDE=90°, ∴BD⊥AC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
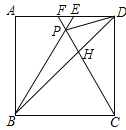
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
①△ABE≌△DCF;②![]() ;③DP2=PHPB;④
;③DP2=PHPB;④![]() .
.
其中正确的是____________.(写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设y=kx,是否存在实数k,使得代数式(x2﹣y2)(4x2﹣y2)+3x2(4x2﹣y2)能化简为x4?若能,请求出所有满足条件的k的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=24cm,P、Q、M、N分别从A、B、C、D出发,沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止、已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm,
(1)当x为何值时,点P、N重合;
(2)当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com