练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
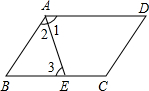
    18．如图所示，在平行四边形ABCD中，∠BAD的平分线AE分对边长度为3和4两部分，求四边形ABCD的周长．

    分析 由在平行四边形ABCD中，∠BAD的平分线AE分对边长度为3和4两部分，易得BC=AD=7，△ABE是等腰三角形，然后分别从BE=3或4去分析求解即可求得答案．

    解答 解：∵在平行四边形ABCD中，∠BAD的平分线AE分对边长度为3和4两部分，
    ∴BC=AD=3+4=7，AD∥BC，AB=CD，∠1=∠2，
    ∴∠1=∠3，
    ∴∠2=∠3，
    ∴AB=BE，
    若BE=3，则AB=CD=3，此时四边形ABCD的周长为：2×（3+7）=20；
    若BE=4，则AB=CD=4，此时四边形ABCD的周长为：2×（4+7）=22；
    ∴四边形ABCD的周长为20或22．

    点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质．注意证得△ABE是等腰三角形是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．如图，在矩形ABCD中，对角线AC的垂直平分线EF分别与边AD、BC相交于E、F，垂足为O，连接AF、CE．
    （1）求证：四边形AFCE是菱形；
    （2）若AB=4，BC=8，求菱形AFCE的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

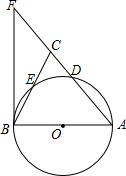    9．如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F．
    （1）求证：∠CBF=$\frac{1}{2}$∠CAB；
    （2）连接BD，AE交于点H，若AB=5，tan∠CBF=$\frac{1}{2}$，求BH的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在△ABC中，∠B=90°，以AB为直径的⊙O交AC于D，点E为BC的中点，连接DE、AE，AE交⊙O于点F．
    （1）求证：DE是⊙O的切线；
    （2）若⊙O的直径为2，求AD•AC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

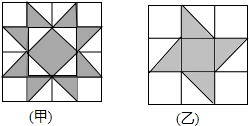    13．如图，有甲、乙两种地板样式，如果小球分别在上面自由滚动，设小球在甲种地板上最终停留在黑色区域的概率为P1，在乙种地板上最终停留在黑色区域的概率为P2，则（　　）
    A．P1＞P2B．P1＜P2C．P1=P2D．以上都有可能

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

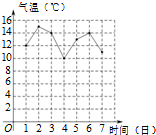    3．右图是某市10月1日至7日一周内“日平均气温变化统计图”．在这组数据中，众数和中位数分别是（　　）
    A．13，13B．14，14C．13，14D．14，13

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．在学习“一次函数与二元一次方程”时，我们知道了两个一次函数图象的交点坐标与其相应的二元一次方程组的解之间的关系，请通过此经验推断：在同一平面直角坐标系中，函数y=5x2-3x+4与y=4x2-x+3的图象交点个数有（　　）
    A．0个B．1个C．2个D．无数个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：（$\frac{1}{2}$）-1+|-2|-2cos60°+（1-π）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知：如图，FE、AB分别是△ACF的边AC、FC上的高，DB=BC．求证：AB=BF．

    查看答案和解析>>

    同步练习册答案