
【题目】如图①,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在AD、AF上,此时BD=CF,BD⊥CF成立.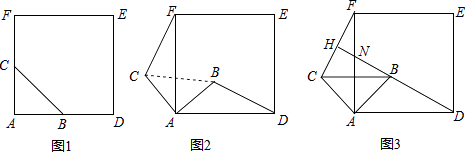
(1)如图②,
i)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,线段BD与线段CF的数量关系是;直线BD与直线CF的位置关系是 .
ii)请利用图②证明上述结论.
(2)如图③,当△ABC绕点A逆时针旋转45°时,延长DB交CF于点H,若AB= ![]() ,AD=3时,求线段FC的长.
,AD=3时,求线段FC的长.
【答案】
(1)BD=CF,BD⊥CF
(2)如图3,过点B作BP⊥AD于P,
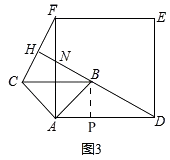
由旋转知,∠BAD=45°,
在Rt△ABP中,AB= ![]() ,
,
∴AP=BP=1,
∴DP=AD﹣AP=2,
在Rt△BDP中,根据勾股定理得,BD= ![]() =
= ![]() ,
,
由(1)知,FC=BD= ![]() .
.
【解析】解:(1)、i)BD=CF,BD⊥CF,
所以答案是:BD=CF,BD⊥CF;
ii)证明:如图2,延长DB交AF于点M,交CF于点N,
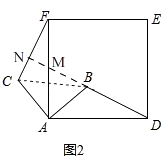
在正方形ADEF中,AD=AF,∠FAD=∠CBA=90°,
在△ABD和△ACF中, 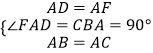 ,
,
∴△ABD≌△ACF(SAS),
∴BD=CF,∠ADB=∠AFC,
∵∠ADB+∠AMD=90°,
∴∠ADB+∠AMD=90°,
∴∠AFC+∠AMD=90°,
∵∠AMD=∠FMN,
∴∠AFC+∠FMN=90°,
∴∠FND=90°,
∴BD⊥CF;


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,过点D作DE∥AB,交BC于E,且DE=BC,连接AC交AC于F,若∠ACB=∠CDE=30°,则图中有几个等腰三角形?请找出来并说明理由. 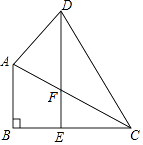
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为cm. 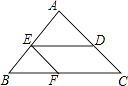
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学质量检测试题中,有一道分值为8分的解答题,所有考生的得分只有四种,即:0分,3分,5分,8分,老师为了解本题学生得分情况,从全区4500名考生试卷中随机抽取一部分,分析、整理本题学生得分情况并绘制了如下两幅不完整的统计图:
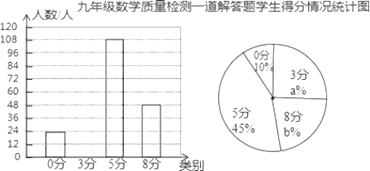
请根据以上信息解答下列问题:
(1)本次调查从全区抽取了 份学生试卷;扇形统计图中a= ,b= ;
(2)补全条形统计图;
(3)该地区这次九年级数学质量检测中,请估计全区考生这道8分解答题的平均得分是多少?得8分的有多少名考生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生就校园安全知识的了解程度,进行了随机抽样调查,并根据学生的成绩划分为A(熟悉)、B(基本了解)、C(略有知晓)、D(知之甚少)四个等次,绘制成如图所示的两幅统计图.
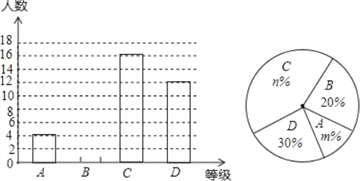
请根据以上信息回答下列问题:
(1)分别求出统计图中m,n的值;
(2)估计该校2350名学生中为A(熟悉)和B(基本了解)档次的学生共有多少人;
(3)从被调查的“熟悉”档次的学生中随机抽取2人,参加市举办的校园安全知识竞赛,请用列表或画树状图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF. 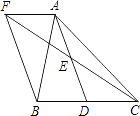
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个图形和它经过平移所得的图形中,两组对应点所连的线段的关系是( )
A.平行B.相等
C.平行(或在同一条直线上)且相等D.既不平行,又不相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com