
【题目】在△ABC中,AB=13,AC=5,BC边上的中线AD=6,点E在AD的延长线上,且ED=AD.
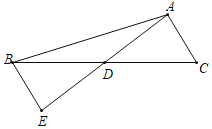
(1)求证:BE∥AC;
(2)求∠CAD的大小;
(3)求点A到BC的距离.
【答案】(1)证明见解析;(2)90°;(3)![]() .
.
【解析】
(1)先证明△ADC≌△EDB,可得∠CAD=∠BED,进而可得结论;
(2)由勾股定理逆定理可得△ABE是直角三角形,∠E=90°,进而可得∠CAD=∠E=90°;
(3)先由勾股定理求CD,再由AFCD=ACAD可求AF即可.
解:(1)证明:∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△EDB中,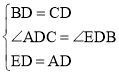 ,
,
∴△ADC≌△EDB(SAS),
∴∠CAD=∠BED,
∴BE∥AC.
(2)∵△ADC≌△EDB,
∴BE=AC=5,
在△ABE中,∵AB=13,BE=5,AE=2AD=12,
∴AE2+BE2=122+52=169,AB2=132=169,
∴AE2+BE2=AB2
∴∠E=90°,
∵BE∥AC,
∴∠CAD=∠E=90°;
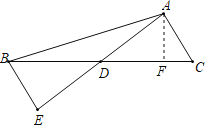
(3)如图,过点A作AF⊥BC于F,
在Rt△ACD中,CD=![]() =
=![]() =
=![]() ,
,
∵AFCD=ACAD,
∴AF=![]() =
=![]() =
=![]() ,
,
即点A到BC的距离为![]() .
.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,AB=4,点G是射线AB上的一个动点,以DG为边向右作正方形DGEF,作EH⊥AB于点H.
(1)若点G在点B的右边.试探索:EH![]() BG的值是否为定值,若是,请求出定值;若不是,请说明理由.
BG的值是否为定值,若是,请求出定值;若不是,请说明理由.

(2)连接EB,在G点的整个运动(点G与点A重合除外)过程中,求∠EBH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明每天上午9时骑自行车离开家,15时回家,他描绘了离家的距与时间的变化情况.
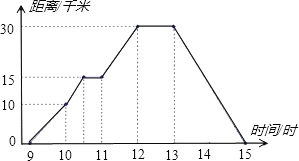
(1)图象表示哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方时什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他由离家最远的地方返回的平均速度是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年12月16日,南京大报恩寺遗址公园正式对外开放.某校数学兴趣小组想测量大报恩塔的高度.如图,成员小明利用测角仪在B处测得塔顶的仰角α=63.5°,然后沿着正对该塔的方向前进了13.1m到达E处,再次测得塔顶的仰角β=71.6°.测角仪BD的高度为1.4m,那么该塔AC的高度是多少?(参考数据:sin63.5°≈0.90,cos63.5°≈0.45,tan63.5°≈2.00,sin71.6°≈0.95,cos71.6°≈0.30,tan71.6°≈3.00)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)求三辆车全部同向而行的概率;
(2)求至少有两辆车向左转的概率;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为![]() ,向左转和直行的频率均为
,向左转和直行的频率均为![]() .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A. 中位数是6.5 B. 平均数高于众数
C. 极差为3 D. 平均每周锻炼超过6小时的人占总数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,它是把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,将这种做法继续下去(如图2,图3…).观察规律解答以下各题:
 ……
……
(1)填写下表:
图形序号 | 挖去三角形的个数 |
图1 | 1 |
图2 | 1+3 |
图3 | 1+3+9 |
图4 |
(2)根据这个规律,求图n中挖去三角形的个数fn(用含n的代数式表示);
(3)若图n+1中挖去三角形的个数为fn+1,求fn+1-fn
查看答案和解析>>
科目:初中数学 来源: 题型:
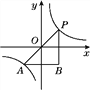
【题目】反比例函数y=![]() 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+![]() =0的根的情况是________________.
=0的根的情况是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com