
【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
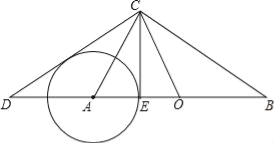
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD=![]() ,BC=10,求CE的长;
,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
【答案】(1)详见解析;(2)(i)CE=6![]() ;(ii)详见解析.
;(ii)详见解析.
【解析】
试题分析:(1)因为∠ACB=∠DCO=90°,所以∠ACD=∠OCB,又因为点O是Rt△ACB中斜边AB的中点,所以OC=OB,所以∠OCB=∠B,利用等量代换可知∠ACD=∠B;(2)(i)因为BC2=ABBE,所以△ABC∽△CBE,所以∠ACB=∠CEB=90°,因为tan∠ACD=tan∠B,利用勾股定理即可求出CE的值;(ii)过点A作AF⊥CD于点F,易证∠DCA=∠ACE,即可得CA是∠DCE的平分线,所以AF=AE,所以直线CD与⊙A相切.
试题解析:(1)∵∠ACB=∠DCO=90°,
∴∠ACB﹣∠ACO=∠DCO﹣∠ACO,
即∠ACD=∠OCB,
又∵点O是AB的中点,
∴OC=OB,
∴∠OCB=∠B,
∴∠ACD=∠B,
(2)(i)∵BC2=ABBE,
∴![]() ,
,
∵∠B=∠B,
∴△ABC∽△CBE,
∴∠ACB=∠CEB=90°,
∵∠ACD=∠B,
∴tan∠ACD=tan∠B=![]() ,
,
设BE=4x,CE=3x,
由勾股定理可知:BE2+CE2=BC2,
∴(4x)2+(3x)2=100,
∴解得x=2![]() ,
,
∴CE=6![]() ;
;
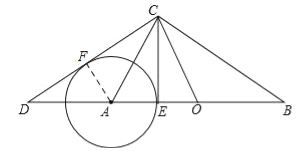
(ii)过点A作AF⊥CD于点F,
∵∠CEB=90°,
∴∠B+∠ECB=90°,
∵∠ACE+∠ECB=90°,
∴∠B=∠ACE,
∵∠ACD=∠B,
∴∠ACD=∠ACE,
∴CA平分∠DCE,
∵AF⊥CE,AE⊥CE,
∴AF=AE,
∴直线CD与⊙A相切.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 平移不改变图形的形状,旋转使图形的形状发生改变
B. 平移和旋转的共同之处是改变图形的位置和大小
C. 一对对应点与旋转中心的距离相等
D. 由旋转得到的图形也一定可以通过平移得到
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:新京报讯(记者沙璐摄影彭子洋)5月7日,第五届北京农业嘉年华圆满闭幕.历时58天的会期,共接待游客136.9万人次,累计实现总收入3.41亿元.其中4月3日的接待量为10.6万人次,创下了五届农业嘉年华以来单日游客人数的最高纪录.
本届北京农业嘉年华共打造了180余个创意景观,汇集了680余个农业优新特品种、130余项先进农业技术,开展了210余项娱乐游艺和互动体验活动. 在去年“三馆两园一带一谷”的基础上,增设了“一线”,即京北旅游黄金线,并在草莓博览园作为主会场的同时,首设乐多港、延寿两大分会场.
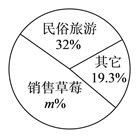
据统计,本届嘉年华期间共有600余家展商参展,设置了1700处科普展板,近6万人参与“草莓票香”体验活动,周边各草莓采摘园接待游客达267万人次,销售草莓265.6万公斤,实现收入1.659亿元.同时,还有效带动延寿、兴寿、小汤山、崔村、百善、南邵6个镇的民俗旅游,实现收入1.09亿元,较上届增长14.84%.
根据以上材料回答下列问题:
(1)举办农业嘉年华以来单日游客人数的最高纪录是 ;
(2)如右图,用扇形统计图表示民俗旅游、销售草莓及其它方面收入的分布情况,则m= ;
(3)选择统计表或统计图,将本届嘉年华的创意景观、农业优新特品种、展商参展、科普展板的数量表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学竞赛共有20道选择题。评分标准为:答对1道题给5分,答错1道题扣3分,不答题不给分也不扣分。小华有3道题未做,则他至少答对______道题,总分才不会低于65分。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com