
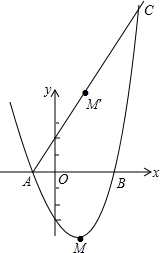
 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.分析 (1)根据待定系数法,可得函数解析式;
(2)根据轴对称,可得M′的坐标,根据待定系数法,可得AM′的解析式,根据解方程组,可得C点坐标,根据三角形的面积公式,可得答案;
(3)根据正方形的性质,可得P、Q点坐标,根据待定系数法,可得函数解析式.
解答 解:(1)将A、B点坐标代入函数解析式,得$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
抛物线的解析式y=x2-2x-3;
(2)将抛物线的解析式化为顶点式,得
y=(x-1)2-4,
M点的坐标为(1,-4),
M′点的坐标为(1,4),
设AM′的解析式为y=kx+b,
将A、M′点的坐标代入,得
$\left\{\begin{array}{l}{-k+b=0①}\\{k+b=4②}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$,
AM′的解析式为y=2x+2,
联立AM′与抛物线,得
$\left\{\begin{array}{l}{y=x+2}\\{y={x}^{2}-2x-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=5}\\{{y}_{2}=12}\end{array}\right.$
C点坐标为(5,12).
S△ABC=$\frac{1}{2}$×4×12=24;
(3)存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形,
由ABPQ是正方形,A(-1,0)B(3,0),得
P(1,-2),Q(1,2),或P(1,2),Q(1,-2),
①当顶点P(1,-2)时,设抛物线的解析式为y=a(x-1)2-2,
将A点坐标代入函数解析式,得
a(-1-1)2-2=0,
解得a=$\frac{1}{2}$,
抛物线的解析式为y=$\frac{1}{2}$(x-1)2-2,
②当P(1,2)时,设抛物线的解析式为y=a(x-1)2+2,将
A点坐标代入函数解析式,得
a(-1-1)2+2=0,
解得a=-$\frac{1}{2}$,
抛物线的解析式为y=-$\frac{1}{2}$(x-1)2+2,
综上所述:y=$\frac{1}{2}$(x-1)2-2或y=-$\frac{1}{2}$(x-1)2+2,使得四边形APBQ为正方形.
点评 本题考查了二次函数综合题,(1)利用待定系数法求函数解析式;(2)利用轴对称的性质得出M′的解析式,利用待定系数法得出AM′的解析式,利用解方程组得出C点坐标是解题关键;(3)利用正方形的性质得出P、Q点坐标是解题关键,又利用待定系数法求函数解析式,注意要分类讨论,以防遗漏.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A,B两点.
如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
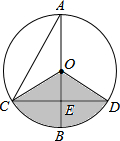 如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )
如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )| A. | $\frac{2\sqrt{3}π}{9}$ | B. | $\frac{4\sqrt{3}π}{9}$ | C. | $\frac{2π}{9}$ | D. | $\frac{4π}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
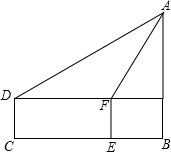 小丽为了测旗杆AB的高度,小丽眼睛距地面1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.
小丽为了测旗杆AB的高度,小丽眼睛距地面1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
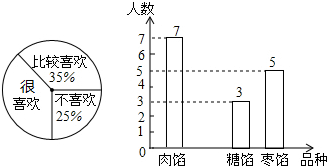
 课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.| 等级 | 人数/名 |
| 优秀 | a |
| 良好 | b |
| 及格 | 150 |
| 不及格 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{a-b}$ | B. | $\frac{b}{a-b}$ | C. | $\frac{a}{a+b}$ | D. | $\frac{b}{a+b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$)-1=-$\frac{1}{2}$ | B. | 6×107=6000000 | C. | (2a)2=2a2 | D. | a3•a2=a5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com