
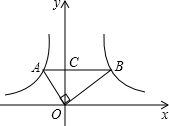
 如图,在函数y1=
如图,在函数y1=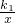 (x<0)和y2=
(x<0)和y2=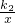 (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC= ,S△BOC=
,S△BOC= ,则线段AB的长度=________.
,则线段AB的长度=________.
 (k≠0)系数k的几何意义易得两反比例解析式为y=-
(k≠0)系数k的几何意义易得两反比例解析式为y=- ,y=
,y= ,设B点坐标为(
,设B点坐标为(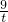 ,t)(t>0),则可表示出A点坐标为(-
,t)(t>0),则可表示出A点坐标为(- ,t),然后证明Rt△AOC∽Rt△OBC,得到OC:BC=AC:BC,即t:
,t),然后证明Rt△AOC∽Rt△OBC,得到OC:BC=AC:BC,即t: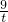 =
= :t,解得t=
:t,解得t= ,再确定A、B点的坐标,最后用两点的横坐标之差来得到线段AB的长.
,再确定A、B点的坐标,最后用两点的横坐标之差来得到线段AB的长. ,S△BOC=
,S△BOC= ,
, |k1|=
|k1|= ,
, |k2|=
|k2|= ,
, ,y=
,y= ,
,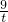 ,t)(t>0),
,t)(t>0), 得x=-
得x=- ,
, ,t),
,t),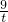 =
= :t,
:t, ,
, ,
, ),B点坐标为(3
),B点坐标为(3 ,
, ),
), -(-
-(- )=
)= .
. .
. (k≠0)系数k的几何意义:从反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y= (k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|. 

科目:初中数学 来源: 题型:
 如图,反比例函数y1=
如图,反比例函数y1=| m | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•眉山)如图,在函数y1=
(2013•眉山)如图,在函数y1=| k1 |
| x |
| k2 |
| x |
| 1 |
| 2 |
| 9 |
| 2 |
10
| ||
| 3 |
10
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源:2013年四川省眉山市中考数学试卷(解析版) 题型:填空题
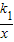 (x<0)和y2=
(x<0)和y2=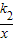 (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC= ,S△BOC=
,S△BOC= ,则线段AB的长度= .
,则线段AB的长度= .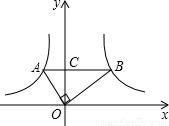
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com