
【题目】如图,已知直线l:y1=kx+b分别与x轴、y轴交于A、B两点,与双曲线y2=![]() (a≠0,x>0)分别交于D、E两点.若点D的坐标为(4,1),点E的坐标为(1,4)
(a≠0,x>0)分别交于D、E两点.若点D的坐标为(4,1),点E的坐标为(1,4)

(1) 分别直接写出直线l与双曲线的解析式:
(2) 若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点
(3) 当y1<y2时,直接写出x的取值范围
【答案】(1)反比例函数解析式为y=![]() (x>0);直线l的解析式为y=-x+5;(2)当m=1时,直线l与双曲线有且只有一个交点;(3)当x<1或x>4时,y1<y2.
(x>0);直线l的解析式为y=-x+5;(2)当m=1时,直线l与双曲线有且只有一个交点;(3)当x<1或x>4时,y1<y2.
【解析】
试题分析:(1)①运用待定系数法可分别得到直线l与双曲线的解析式;
②直线l向下平移m(m>0)个单位得到y=-x+5-m,根据题意得方程组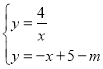 只有一组解时,化为关于x的方程得x2+(m-5)x+4=0,则△=(m-5)2-4×4=0,解得m1=1,m2=9,当m=9时,公共点不在第一象限,所以m=1;
只有一组解时,化为关于x的方程得x2+(m-5)x+4=0,则△=(m-5)2-4×4=0,解得m1=1,m2=9,当m=9时,公共点不在第一象限,所以m=1;
(3)解方程组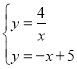 即可求解.
即可求解.
试题解析:(1)①把D(4,1)代入y=![]() 得a=1×4=4,
得a=1×4=4,
所以反比例函数解析式为y=![]() (x>0);
(x>0);
设直线l的解析式为y=kx+t,
把D(4,1),E(1,4)代入得![]() ,
,
解得![]() .
.
所以直线l的解析式为y=-x+5;
②直线l向下平移m(m>0)个单位得到y=-x+5-m,
当方程组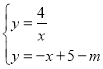 只有一组解时,直线l与双曲线有且只有一个交点,
只有一组解时,直线l与双曲线有且只有一个交点,
化为关于x的方程得x2+(m-5)x+4=0,
△=(m-5)2-4×4=0,解得m1=1,m2=9,
而m=9时,解得x=-2,故舍去,
所以当m=1时,直线l与双曲线有且只有一个交点;
(3)解方程组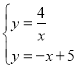 得:x1=1,x2=4
得:x1=1,x2=4
故当x<1或x>4时,y1<y2.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
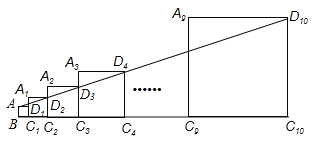
【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推…,若A1C1=2,且点A,D2, D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中,一定成立的是( )
A. AB=CD B. AB≤CD C. AB≥CD D. AB>CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com