
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值及数的开方法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.
解答 解:(1)原式=4+|$\frac{1}{2}$-1|+1+$\frac{1}{4}$
=4+$\frac{1}{2}$+$\frac{1}{4}$
=4$\frac{3}{4}$;
(2)原式=$\frac{1}{x+1}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{x-1}{x}$,
当x=2时,原式=$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
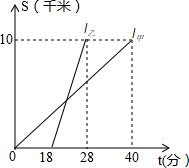 某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.
某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
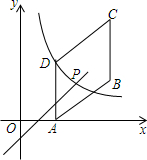 如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点.对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,则点P横坐标a的取值范围$\frac{2}{3}$<a<3.
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点.对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,则点P横坐标a的取值范围$\frac{2}{3}$<a<3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com