
分析 (1)设这种服装提价x元,首先用代数式表示出每件的盈利,以及可销售的件数,根据每件的盈利×销售的件数=获利12000元,即可列方程求解;
(2)根据(1)中的等量关系,可得出关于总利润和调高的价格的函数关系式,然后根据函数的性质,求出函数的最大值.
解答 解:(1)设这种服装提价x元,
由题意得:(60-50+x)(800-20x)=12000,
解这个方程得:x1=10,x2=20.
当x1=10时,800-20×10=600,50×600=30 000>24 000,舍去;
故x=20,800-20×20=400,60+20=80.
答:这种服装销售单价确定为80元为宜,这时应进400件服装;
(2)设利润为y=(10+x)(800-20x)=-20(x-15)2+12500,
当x=15,定价为60+x=75元时,可获得最大利润:12500元.
点评 本题主要考查了二次函数的实际应用,读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
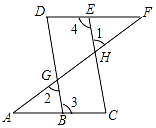 如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
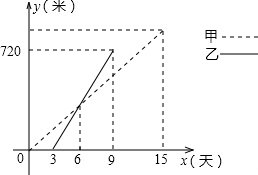 如皋某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
如皋某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 38 | B. | 44 | C. | 65 | D. | 73 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
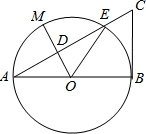 如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$ 的中点,OM交AC于点D,BC=2$\sqrt{3}$,∠BOE=60°,∠C=60°.
如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$ 的中点,OM交AC于点D,BC=2$\sqrt{3}$,∠BOE=60°,∠C=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com