
【题目】如图,已知抛物线y=x2+bx+c与直线y=﹣x+3相交于坐标轴上的A,B两点,顶点为C.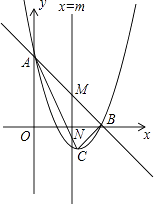
(1)填空:b= , c=;
(2)将直线AB向下平移h个单位长度,得直线EF.当h为何值时,直线EF与抛物线y=x2+bx+c没有交点?
(3)直线x=m与△ABC的边AB,AC分别交于点M,N.当直线x=m把△ABC的面积分为1:2两部分时,求m的值.
【答案】
(1)﹣4,3
(2)解:∵将直线AB:y=﹣x+3向下平移h个单位长度,得直线EF,
∴可设直线EF的解析式为y=﹣x+3﹣h.
把y=﹣x+3﹣h代入y=x2﹣4x+3,得x2﹣4x+3=﹣x+3﹣h.
整理得:x2﹣3x+h=0.
∵直线EF与抛物线没有交点,
∴△=(﹣3)2﹣4×1×h=9﹣4h<0,
解得h> ![]() .
.
∴当h> ![]() 时,直线EF与抛物线没有交点;
时,直线EF与抛物线没有交点;
(3)解:∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点C(2,﹣1).
设直线AC的解析式为y=mx+n.
则 ![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为y=﹣2x+3.
如图,设直线AC交x轴于点D,则D( ![]() ,0),BD=
,0),BD= ![]() .
.
∴S△ABC=S△ABD+S△BCD= ![]() ×
× ![]() ×3+
×3+ ![]() ×
× ![]() ×1=3.
×1=3.
∵直线x=m与线段AB、AC分别交于M、N两点,则0≤m≤2,
∴M(m,﹣m+3),N(m,﹣2m+3),
∴MN=(﹣m+3)﹣(﹣2m+3)=m.
∵直线x=m把△ABC的面积分为1:2两部分,
∴分两种情况讨论:
①当 ![]() =
= ![]() 时,即
时,即 ![]() =
= ![]() ,解得 m=±
,解得 m=± ![]() ;
;
②当 ![]() =
= ![]() 时,即
时,即 ![]() =
= ![]() ,解得 m=±2
,解得 m=±2
∵0≤m≤2,
∴m= ![]() 或m=2.
或m=2.
∴当m= ![]() 或2时,直线x=m把△ABC的面积分为1:2两部分.
或2时,直线x=m把△ABC的面积分为1:2两部分.
【解析】解:(1)∵直线y=﹣x+3交坐标轴于A,B两点,
∴A(0,3),B(3,0),
把A(0,3),B(3,0)代入y=x2+bx+c,
得 ![]() ,解得
,解得 ![]() .
.
所以答案是﹣4,3;


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式因式分解.例如:![]() ,
,![]() 都是因式分解.因式分解也可称为分解因式.
都是因式分解.因式分解也可称为分解因式.
材料2:只含有一个未知数,且未知数的最高次数是![]() 的整式方程称作一元二次方程.一元二次方程的般形式是:
的整式方程称作一元二次方程.一元二次方程的般形式是:![]() (其中
(其中![]() ,
,![]() ,
,![]() 为常数且
为常数且![]() ).“转化”是一种重要的数学思想方法,我们可以利用因式分解把部分一元二次方程转化为一元一次方程求解.
).“转化”是一种重要的数学思想方法,我们可以利用因式分解把部分一元二次方程转化为一元一次方程求解.
例如解方程;![]()
![]()
![]()
![]() 或
或![]()
![]() 原方程的解是
原方程的解是![]() ,
,![]()
∴原方程的解是![]() ,
,![]()
又如解方程:![]()
![]()
![]()
![]()
![]() 原方程的解是
原方程的解是![]()
请阅读以上材料回答以下问题:
(1)若![]() ,则
,则![]() _______;
_______;![]() _______;
_______;
(2)请将下列多项式因式分解:
![]() _______,
_______,![]() ________;
________;
(3)在平面直角坐标系中,已知点![]() ,
,![]() ,其中
,其中![]() 是一元二次方程
是一元二次方程![]() 的解,
的解,![]() 为任意实数,求
为任意实数,求![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.

(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )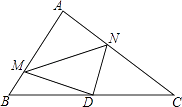
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )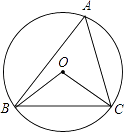
A.3 ![]()
B.4 ![]()
C.5 ![]()
D.6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了创建书香校园,去年购买了一批图书.其中科普书的单价比文学书的单价多4元,用1200元购买的科普书与用800元购买的文学书本数相等.
(1)求去年购买的文学书和科普书的单价各是多少元?
(2)若今年文学书的单价比去年提高了25%,科普书的单价与去年相同,为了普及科普知识,书店举办了每买三本科普书就赠一本文学书的优惠活动,这所中学今年计划在优惠活动期间,再购进文学书和科普书共200本,且购买文学书和科普书的总费用不超过1880元,这所中学今年最多能购进多少本文学书?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com