
分析 根据已知条件可以画出相应的图形,然后根据勾股定理可以求得各边的长度,从而可以解答本题.
解答 解:如下图所示: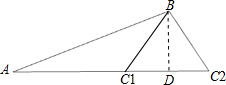
根据题意分两种情况,
第一种情况是在△ABC1中,作BD⊥AC1交AC1的延长线于点D,
∵AB=$\sqrt{10}$,BC=$\sqrt{2}$,tanA=$\frac{1}{3}$,
∴设BD=x,则AD=3x,${x}^{2}+(3x)^{2}=(\sqrt{10})^{2}$.
得,BD=1,AD=3.
∴D${C}_{1}=\sqrt{B{{C}_{1}}^{2}-B{D}^{2}}=\sqrt{(\sqrt{2})^{2}-{1}^{2}}$=1.
∴AC1=AD-AC1=2.
第二种情况是在△ABC2中,作BD⊥AC2交AC2的延长线于点D,
∵AB=$\sqrt{10}$,BC=$\sqrt{2}$,tanA=$\frac{1}{3}$,
∴设BD=x,则AD=3x,${x}^{2}+(3x)^{2}=(\sqrt{10})^{2}$.
得,BD=1,AD=3.
∴$D{C}_{2}=\sqrt{B{{C}_{2}}^{2}-B{D}^{2}}=\sqrt{(\sqrt{2})^{2}-{1}^{2}}=1$.
∴AC2=AD+DC2=4.
故答案为:2或4.
点评 本题考查解直角三角形,解题的关键是能画出相应的图形,考虑问题一定要全面.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
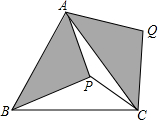 如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )
如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )| A. | 70° | B. | 80° | C. | 60° | D. | 50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com