
【题目】某幼儿园对全体小朋友爱吃哪种粽子做调查,以决定最终买哪种口味的粽子.下面的调查数据最值得关注的是( )
A.方差
B.平均数
C.中位数
D.众数
科目:初中数学 来源: 题型:
【题目】所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式。心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质。我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如下图表:
四种气质类型人数频数分布表 | 黏液质气质各年级人数频数分布直方图 | |||||||||||||||
|
|
根据以上信息完成下列问题并补全频数分布直方图:
(1)![]() _______,
_______, ![]() _______
_______
(2)请你估计一下,高三年级1200名学生中,胆汁型和多血质的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一支原长为20cm的蜡烛,点燃后,其剩余长度y(cm)与燃烧时间x(min)之前的关系如表:
燃烧时间x(min) | 10 | 20 | 30 | 40 | 50 | … |
剩余长度y(cm) | 19 | 18 | 17 | 16 | 15 | … |
(1)表中反映的自变量是什么?因变量是什么?
(2)求出剩余长度y(cm)与燃烧时间x(min)之间的关系式;
(3)估计这支蜡烛最多可燃烧多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
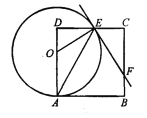
【题目】如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于 点F,且∠CEF=2∠DAE.
(1)求证:直线EF为⊙O的切线;
(2)在点O的运动过程中,设DE=x,解决下列问题:
①求OD·CF的最大值,并求此时半径的长;
②试猜想并证明△CEF的周长为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“﹣”,从开始到结束爬行的各段路程(单位:cm)依次为:+7,﹣5,﹣10,﹣8,+9,﹣6,+12,+4
(1)若A点在数轴上表示的数为﹣3,则蜗牛停在数轴上何处,请通过计算加以说明;
(2)若蜗牛的爬行速度为每秒 ![]() cm,请问蜗牛一共爬行了多少秒?
cm,请问蜗牛一共爬行了多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知二次函数的解析式是y=ax2+bx(a>0),顶点为A(1,-1).
(1)a= ;
(2)若点P在对称轴右侧的二次函数图像上运动,连结OP,交对称轴于点B,点B关于顶点A的对称点为C,连接PC、OC,求证:∠PCB=∠OCB;
(3)如图②,将抛物线沿直线y=-x作n次平移(n为正整数,n≤12),顶点分别为A1,A2,…,An,横坐标依次为1,2,…,n,各抛物线的对称轴与x轴的交点分别为D1,D2,…,Dn,以线段AnDn为边向右作正方形AnDnEnFn,是否存在点Fn恰好落在其中的一个抛物线上,若存在,求出所有满足条件的正方形边长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 菱形的对角线垂直且相等
B. 到线段两端点距离相等的点,在线段的垂直平分线上
C. 角的平分线就是角的对称轴
D. 形状相同的两个三角形就是全等三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com