
 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.分析 (1)作∠ACB=90°,BC=$\sqrt{2}$,AC=3$\sqrt{2}$,则△ABC的面积为3;
(2)利用网格特点和旋转的性质弧出点A、B的对应点D、E,然后根据弧长公式计算点A绕着点C旋转的路径长.
解答 解:(1)如图,△ABC为所作;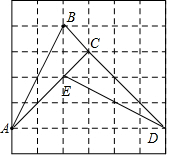
(2)AC=3$\sqrt{2}$,
所以点A绕着点C旋转的路径长=$\frac{90•π•3\sqrt{2}}{180}$=$\frac{3\sqrt{2}}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了勾股定理.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
 如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?
如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点M的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-2 | B. | m>2 | C. | m<-2 | D. | m<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
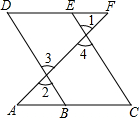 推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com