
 ��y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.
��y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.
 ��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ��
��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ�� ��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵������.
��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵������.
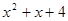 ����2��Q��1��0������3�����ڣ�P1��
����2��Q��1��0������3�����ڣ�P1�� ��2����P2��
��2����P2�� ��2����P3��
��2����P3��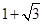 ��3����P4��
��3����P4�� ��3��.
��3��. �����ô���ϵ�������������ĸa��c��ֵ���Ӷ����������ϵʽ����2�����Q������Ϊ��m��0��������EQ��AC���õ���BQE�ס�BAC���������������ζ�Ӧ�ߵıȵ������Ʊȣ�����ĸm��ʾ��BG�ij���Ȼ�����
�����ô���ϵ�������������ĸa��c��ֵ���Ӷ����������ϵʽ����2�����Q������Ϊ��m��0��������EQ��AC���õ���BQE�ס�BAC���������������ζ�Ӧ�ߵıȵ������Ʊȣ�����ĸm��ʾ��BG�ij���Ȼ�����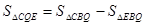 ��ʾ����CQE����ǹ�����ĸm�Ķ��κ��������ݶ��κ��������ʼ������������ֵ����3���������⣬������������Ȼ���ͼ�Σ�Ȼ����ݵ��������ε����ʽ��.
��ʾ����CQE����ǹ�����ĸm�Ķ��κ��������ݶ��κ��������ʼ������������ֵ����3���������⣬������������Ȼ���ͼ�Σ�Ȼ����ݵ��������ε����ʽ��. ��
��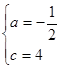

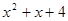 .
.
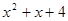 =0����
=0���� =��2��
=��2�� .
. .
. .
.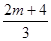 .
.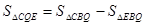



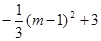 .
. �����ֵΪ3����ʱQ��1��0��.
�����ֵΪ3����ʱQ��1��0��.
 ��x1��
��x1�� ��x2��
��x2��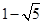 .
. ��2����P��
��2����P�� ��2��.
��2��.
 OD��1.
OD��1. ��x1��
��x1��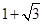 ��x2��
��x2�� .
.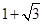 ��3����P��
��3����P�� ��3��.
��3��.
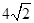 .
. .
. ����OF��
����OF�� ì�ܣ�
ì�ܣ� ��2����P2��
��2����P2�� ��2����P3��
��2����P3��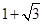 ��3����P4��
��3����P4�� ��3��.
��3��.


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
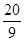 ��,����Ȧ���ĵ�ˮƽ����Ϊ8��,������ֺ�ˮƽ����Ϊ4��ʱ�������߶�4��,���������еĹ켣Ϊ������,��Ȧ���ľ������3��.
��,����Ȧ���ĵ�ˮƽ����Ϊ8��,������ֺ�ˮƽ����Ϊ4��ʱ�������߶�4��,���������еĹ켣Ϊ������,��Ȧ���ľ������3��.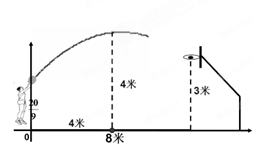
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A����3��1�� | B����3����1�� | C������3��1�� | D������3����1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��x�ύ�ڵ�A��B����A�������Ϊ��1��0������y�ύ�ڵ�C��0��1����
��x�ύ�ڵ�A��B����A�������Ϊ��1��0������y�ύ�ڵ�C��0��1����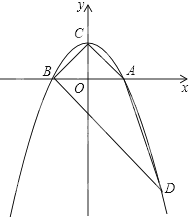
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
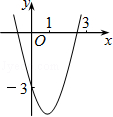
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
A�� | B�� |
C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��
��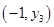 ��
�� �Ĵ�С��ϵΪ�� ��
�Ĵ�С��ϵΪ�� ��A�� | B�� | C�� | D�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com