
 与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).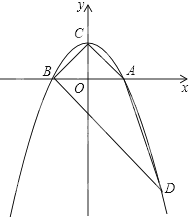
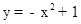 ,B(﹣1,0);(2)
,B(﹣1,0);(2)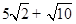 ;(3)存在,P(
;(3)存在,P( ,
,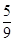 ).
). 上,∴
上,∴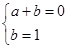 ,解得:a=﹣1,b=1,∴抛物线的解析式为:
,解得:a=﹣1,b=1,∴抛物线的解析式为: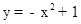 ,抛物线的对称轴为y轴,则点B与点A(1,0)关于y轴对称,∴B(﹣1,0);
,抛物线的对称轴为y轴,则点B与点A(1,0)关于y轴对称,∴B(﹣1,0);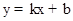 ,可得:
,可得: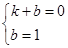 ,解得k=﹣1,b=1,∴
,解得k=﹣1,b=1,∴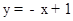 .∵BD∥CA,∴可设直线BD的解析式为
.∵BD∥CA,∴可设直线BD的解析式为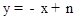 ,∵点B(﹣1,0)在直线BD上,∴
,∵点B(﹣1,0)在直线BD上,∴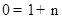 ,得
,得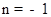 ,∴直线BD的解析式为:
,∴直线BD的解析式为: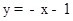 .将
.将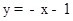 代入抛物线的解析式,得:
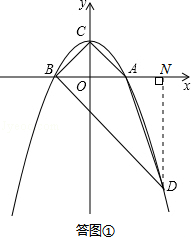
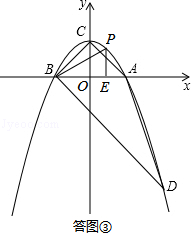
代入抛物线的解析式,得: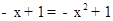 ,解得:x1=2,x2=﹣1,∵B点横坐标为﹣1,则D点横坐标为2,D点纵坐标为y=﹣2﹣1=﹣3,∴D点坐标为(2,﹣3).如答图①所示,过点D作DN⊥x轴于点N,则DN=3,AN=1,BN=3,在Rt△BDN中,BN=DN=3,由勾股定理得:BD=
,解得:x1=2,x2=﹣1,∵B点横坐标为﹣1,则D点横坐标为2,D点纵坐标为y=﹣2﹣1=﹣3,∴D点坐标为(2,﹣3).如答图①所示,过点D作DN⊥x轴于点N,则DN=3,AN=1,BN=3,在Rt△BDN中,BN=DN=3,由勾股定理得:BD=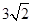 ;在Rt△ADN中,DN=3,AN=1,由勾股定理得:AD=
;在Rt△ADN中,DN=3,AN=1,由勾股定理得:AD=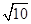 ;又OA=OB=OC=1,OC⊥AB,由勾股定理得:AC=BC=
;又OA=OB=OC=1,OC⊥AB,由勾股定理得:AC=BC=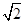 ;∴四边形ABCD的周长为:AC+BC+BD+AD=
;∴四边形ABCD的周长为:AC+BC+BD+AD=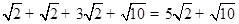 .
.
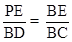 ,即
,即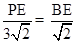 ,∴PE=3BE.设OE=m(m>0),则E(﹣m,0),BE=1﹣m,PE=3BE=3﹣3m,∴点P的坐标为(﹣m,3﹣3m),∵点P在抛物线
,∴PE=3BE.设OE=m(m>0),则E(﹣m,0),BE=1﹣m,PE=3BE=3﹣3m,∴点P的坐标为(﹣m,3﹣3m),∵点P在抛物线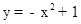 上,∴
上,∴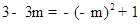 ,解得m=1或m=2,当m=1时,点E与点B重合,故舍去;当m=2时,点E在OB左侧,点P在x轴下方,不符合题意,故舍去.因此,此种情况不存在;
,解得m=1或m=2,当m=1时,点E与点B重合,故舍去;当m=2时,点E在OB左侧,点P在x轴下方,不符合题意,故舍去.因此,此种情况不存在;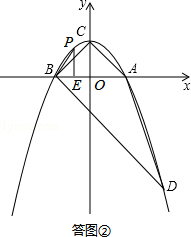
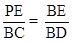 ,即
,即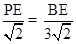 ,∴BE=3PE.设OE=m(m>0),则E(m,0),BE=1+m,PE=
,∴BE=3PE.设OE=m(m>0),则E(m,0),BE=1+m,PE=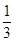 BE=
BE=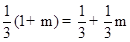 ,∴点P的坐标为(
,∴点P的坐标为( ,
,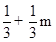 ).∵点P在抛物线
).∵点P在抛物线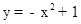 上,∴
上,∴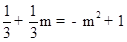 ,解得
,解得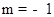 或m=
或m= ,∵m>0,故
,∵m>0,故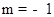 舍去,∴m=
舍去,∴m= ,点P的纵坐标为:
,点P的纵坐标为: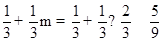 ,∴点P的坐标为(
,∴点P的坐标为( ,
,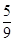 ).
). ,
,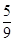 ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线 ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
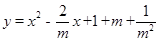 顶点的纵坐标y与横坐标x之间的关系式.
顶点的纵坐标y与横坐标x之间的关系式.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=x2+1 | B.y=(x+1) 2 | C.y=x2-1 | D.y=(x-1) 2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.当x<1时,y随x的增大而减小 | B.它的图象与x轴有交点 |
| C.当1<x<3时,y>0 | D.顶点坐标为(2,-1 ) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图像向左平移2个单位再向下平移4个单位,所得函数表达式是
的图像向左平移2个单位再向下平移4个单位,所得函数表达式是 ,我们来解释一下其中的原因:不妨设平移前图像上任意一点P经过平移后得到点P’,且点P’的坐标为
,我们来解释一下其中的原因:不妨设平移前图像上任意一点P经过平移后得到点P’,且点P’的坐标为 ,那么P’点反之向右平移2个单位,再向上平移4个单位得到点
,那么P’点反之向右平移2个单位,再向上平移4个单位得到点 ,由于点P是二次函数
,由于点P是二次函数 的图像上的点,于是把点P(x+2,y+4)的坐标代入
的图像上的点,于是把点P(x+2,y+4)的坐标代入 再进行整理就得到
再进行整理就得到 .类似的,我们对函数
.类似的,我们对函数 的图像进行平移:先向右平移1个单位,再向上平移3个单位,所得图像的函数表达式为_____.
的图像进行平移:先向右平移1个单位,再向上平移3个单位,所得图像的函数表达式为_____.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.a<0 | B.a﹣b+c<0 |
C. >1 >1 | D.4ac﹣b2<﹣8a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com