Question

8．如图（1），抛物线y=-$\frac{1}{2}$x²+x+4与x轴交于点A，B（点A在点B左侧）、直线l经过点B、C两点
（1）求A、B、C三点坐标及直线BC的函数表达式；
（2）若点F是线段OC上一动点，则在第一象限的抛物线上是否存在点E，使得△BCE≌△BCF，若存在，请直接写出点E的坐标；若不存在，请说明理由．
（3）如图（2），在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以点P、Q、A、M为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

分析 （1）令y=0得到关于x的方程，然后求得方程的解可得到点A和点B的坐标，令y=0求得对应的y值，可求得点C的坐标，设直线BC的解析式为y=kx+b，将点B和点C的坐标代入求得k、b的值即可；
（2）理由：如图1所示：过点C作CE∥x轴，交抛物线与点E，在CO上取点F使得CF=CE．先证明△CEB≌△CFB，然后将点E的纵坐标代入抛物线的解析式求得对应的横坐标的值即可
（3）先求得抛物线的顶点坐标和抛物线的对称轴，则点Q的坐标为横坐标为1，点P的横坐标坐标为x，然后依据平行四边形的对角线互相平分和中点坐标公式可求得点P的横坐标的值，然后将点P的横坐标代入抛物线的解析式可求得点P的纵坐标．

解答 解：（1）当y=0时，-$\frac{1}{2}$x²+x+4=0，解得x₁=-2，x₂=4，
所以点A坐标为（-2，0），点B坐标为（4，0）．
当x=0时，y=4，
所以点C坐标为（0，4）．
设直线BC的解析式为y=kx+b，得$\left\{\begin{array}{l}{4k+b=0}\\{b=4}\end{array}\right.$，
解得k=-1，b=4．
所以直线BC的解析式为y=-x+4．

（2）存在．
理由：如图1所示：过点C作CE∥x轴，交抛物线与点E，在CO上取点F使得CF=CE．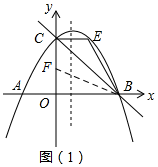

∵CE∥x轴，
∴∠ECO=90°．
∵OC=OB，∠COB=90°，
∴∠OCB=45°．
∴∠ECB=45°．
∴∠FCB=∠ECB．
在△CEB和△CFB中$\left\{\begin{array}{l}{CE=CF}\\{∠FCB=∠ECB}\\{CB=CB}\end{array}\right.$，
∴△CEB≌△CFB．
∵CE∥x轴，
∴点E的纵坐标为4．
将y=4代入抛物线的解析式得：-$\frac{1}{2}$x²+x+4=4，解得：x=2或x=0，
∴E（2，4）．

（3）存在点P，使得以点P，Q，A，M为顶点的四边形是平行四边形．
理由：∵y=-$\frac{1}{2}$x²+x+4=-$\frac{1}{2}$（x-1）²+$\frac{9}{2}$，
∴抛物线的对称轴为直线x=1．
又∵当x=2时，y=-x+4=2，
∴点M的坐标为（2，2）．
设点Q的横坐标1，点P的横坐标为x．
①当AP为平行四边形的对角线时．
由中点坐标公式可得：$\frac{-2+x}{2}$=$\frac{1+2}{2}$，
解得：x=5，
将x=5代入抛物线的解析式得：y=-$\frac{1}{2}$×25+5+4=-$\frac{7}{2}$，
∴P的坐标为（5，-$\frac{7}{2}$）．
②当AQ为平行四边形的对角线时．
由中点坐标公式可得：$\frac{-2+1}{2}$=$\frac{2+x}{2}$，
解得：x=-3．
将x=-3代入得：y=$-\frac{1}{2}$×9-3+4=-$\frac{7}{2}$．
∴点P的坐标为（-3，-$\frac{7}{2}$）．
③当AM为平行四边形的对角线时．
由中点坐标公式可得：$\frac{-2+2}{2}$=$\frac{x+1}{2}$，
解得：x=-1．
将x=-1代入得：y=$-\frac{1}{2}$×1-1+4=$\frac{5}{2}$．
∴点P的坐标为（-1，$\frac{5}{2}$）．
综上所述，当点P的坐标为（5，-$\frac{7}{2}$）、（-3，-$\frac{7}{2}$）或（-1，$\frac{5}{2}$）时，以点P，Q，A，M为顶点的四边形是平行四边形．

点评 本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求一次函数的解析式，全等三角形的性质和判定、等腰直角三角形的性质和判定、平行四边形的性质和判定，线段的中点坐标公式，依据线段的中点坐标公式求得点P的横坐标是解答此类问题的关键．