
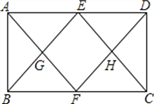
【题目】如图,在矩形ABCD中,E,F分别为AD,BC的中点,连结AF,DF,BE,CE,AF与BE交于G,DF与CE交于H.求证:四边形EGFH为菱形
【答案】证明见解析
【解析】试题分析: 根据一组对边平行且相等的四边形式平行四边形,可证明四边形AECF,BEDF是平行四边形,根据平行四边形的性质,可得GF与EH,EG与FH的关系,根据平行四边形的判定,可得EGFH的形状,根据三角形全等,可得EG与FG的关系,根据菱形的定义,可得证明结论.
试题解析:∵在矩形ABCD中AD=BC,且E,F分别是AD,BC的中点,
∴AE=DE=BF=CF,
又∵AD∥BC,
∴四边形AECF,BEDF是平行四边形,
∴GF∥EH,EG∥FH,
∴四边形EGFH是平行四边形,
在△AEG和△FBG中,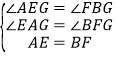 ,
,
∴△AEG≌△FBG(AAS),
∴EG=GB,AG=GF,
在△ABE和△BAF中,
∵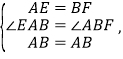
∴△ABE≌△BAF(SAS),
∴AF=BE,
∵EG=GB=![]() BE,AG=GF=
BE,AG=GF=![]() AF,
AF,
∴EG=GF,
∴四边形EGFH是菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
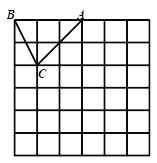
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)与y轴的交点坐标是 , 与x轴的交点坐标是;
(3)在坐标系中利用描点法画出此抛物线.
x | … | … | |||||
y | … | … |
(4)不等式x2﹣2x﹣3>0的解集是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 ,它 (填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚为班级购买了一、二、三等奖的奖品,已知一等奖奖品6元,二等奖奖品4元,三等奖奖品2元,其中获奖人数的分配情况如图,则小刚购买奖品费用的平均数和众数分别为( )%

A. 2元,3元 B. 2.5元,2.5元 C. 3元,2元 D. 3元,3元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面相同的纸牌A,B,C,D,其正面分别是红桃、方块、黑桃、梅花,其中红桃、方块为红色,黑桃、梅花为黑色.小明将这4张纸牌背面朝上洗匀后,摸出一张,将剩余3张洗匀后再摸出一张.请用画树状图或列表的方法求摸出的两张牌均为黑色的概率. 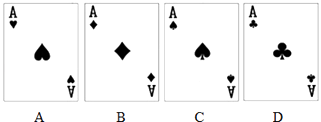
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知x1、x2是方程x2+4x-2=0的两个实数根,求![]() +
+![]() 的值;
的值;
(2)已知方程x2+bx+c=0的两根分别为![]() +1、
+1、![]() -1,求出b、c的值;
-1,求出b、c的值;
(3)关于x的方程x2+(m-1)x+m2-3=0的两个实数根互为倒数,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com