
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
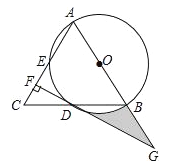
【答案】(1)详见解析;(2)
【解析】(1)连接AD、OD,由AB为直径可得出点D为BC的中点,由此得出OD为△BAC的中位线,再根据中位线的性质即可得出OD⊥DF,从而证出DF是⊙O的切线;
(2)CF=1,DF=![]() ,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
(1)证明:连接AD、OD,如图所示.
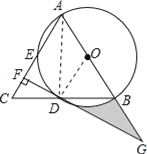
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AC=AB,
∴点D为线段BC的中点.
∵点O为AB的中点,
∴OD为△BAC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线.
(2)解:在Rt△CFD中,CF=1,DF=![]() ,
,
∴tan∠C=![]() =
=![]() ,CD=2,
,CD=2,
∴∠C=60°,
∵AC=AB,
∴△ABC为等边三角形,
∴AB=4.
∵OD∥AC,
∴∠DOG=∠BAC=60°,
∴DG=ODtan∠DOG=2![]() ,
,
∴S阴影=S△ODG﹣S扇形OBD=![]() DGOD﹣
DGOD﹣![]() πOB2=2
πOB2=2![]() ﹣
﹣![]() π.
π.
“点睛”本题考查了等腰三角形的性质、切线的判定、扇形面积的计算以及三角形面积的计算,解题的关键是:(1)证出OD⊥DF;(2)利用分割图形求面积求出阴影部分的面积.本题属于中档题,难度不大,解决该题型题目时,利用分割图形求面积法是解题的难点,在日常练习中应加强训练.


科目:初中数学 来源: 题型:
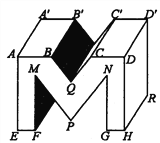
【题目】如图所示,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字“M”:
(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;
(2)EF与A′B′有何位置关系?CC′与DH有何位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办“汉字听写大赛”,7名学生进入决赛,他们所得分数互不相同,比赛共设3个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是(填“平均数”、“众数”或“中位数”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,A、B、C、D 为矩形的四个顶点,AB=16cm,AD=
6cm,动点P、Q 分别从A、C 同时出发,点P 以3cm/s的速度向点B 移动,
一直到达点 B 为止,点 Q 以2cm/s的速度向点 D 移动.
(1)P、Q 两点从出发点出发几秒时,四边形PBCQ 的面积是33cm2?
(2)P、Q 两点从出发点出发几秒时,点P、Q 间的距离是10cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有( ).
①过两点有且只有一条直线;
②连接两点的线段叫两点的距离;
③两点之间线段最短;
④若AC=BC,则点C是线段AB的中点.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南水北调中线工程的起点是丹江口水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位,如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡底端水平方向增加的宽度AC.(结果精确到0.1米,参考数据:sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.5,![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com