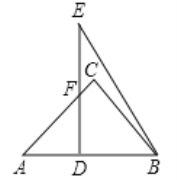
【题目】如图，将两块三角板重叠放置，其中∠C=∠BDE=90°，∠A=45°，∠E=30°，AB=DE=6，求重叠部分四边形DBCF的面积。
【答案】
【解析】
观察可看出，所求四边形的面积等于等腰直角三角形的面积减去S△ADF，从而只要求出这两个三角形的面积即可，这要求我们综合利用解直角三角形，直角三角形的性质和三角函数的灵活运用来解答．
解：在△EDB中，
∵∠BDE=90°，∠E=30°，DE=6，
∴DB=DEtan30°=6×
=2
，
∴AD=AB-DB=6-2．
又∵∠A=45°，∠AFD=45°，得FD=AD．
∴S△ADF=
AD2=×（6-2）2=24-12．
在等腰直角三角形ABC中，斜边AB=6，
∴AC=BC=3
，
∴S△ABC=AC2=9，
∴S四边形DBCF=S△ABC-S△ADF=9-（24-12）=12-15．
故答案为： ．
智能训练练测考系列答案科目：初中数学 来源： 题型：
【题目】已知：直线AB与直线CD交于点O，过点O作OE⊥AB．
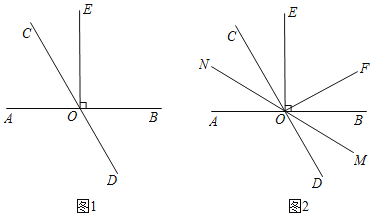
（1）如图1，∠BOC＝2∠AOC，求∠COE的度数；
（2）如图2．在（1）的条件下，过点O作OF⊥CD，经过点O画直线MN，满足射线OM平分∠BOD，在不添加任何辅助线的情况下，请直接写出与2∠EOF度数相等的角．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程（x-3）(x-2)-p2=0.
（1）求证：无论p取何值时，方程总有两个不相等的实数根；
（2）设方程两实数根分别为x1、x2，且满足x12+x22=3 x1x2，求实数p的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在RtΔABC中，AD是斜边BC上的高，∠B=30°，那么线段BD与CD的数量关系为（ ）
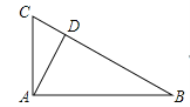
A. BD=CDB. BD=2CDC. BD=3CDD. BD=4CD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】杨辉是中国南宋末年的一位杰出的数学家，数学教育家．杨辉三角是杨辉的一大重要研究成果，其中蕴含了许多优美的规律．古今中外，许多的数学家都曾对其深入研究过，并将研究结果应用于实践．其中杨辉三角如下
（1）第5行的数和为________
（2）观察每行数的和，并归纳出第
行数的和为________
（3）第三斜行的数分别为1，3，6，10，…，请依此规律写出第5个数为 ．请归纳得出第三斜行第个数的表达式________（用含有的表达式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
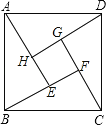
【题目】如图，这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．已知AE=3，BE=2，若向正方形ABCD内随意投掷飞镖（每次均落在正方形ABCD内，且落在正方形ABCD内任何一点的机会均等），则恰好落在正方形EFGH内的概率为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，反比例函数y=
（k＞0）的图象与半径为5的⊙O交于M、N两点，△MON的面积为3.5，若动点P在x轴上，则PM+PN的最小值是_____．
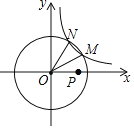
查看答案和解析>>
科目：初中数学 来源： 题型：
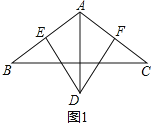
【题目】在△ABC中，AB=AC，∠BAC=120，AD⊥BC，且AD=AB．
（1）如图1，DE⊥AB，DF⊥AC，垂足分别为点E，F，求证：AE+AF=AD
（2）如图2，如果∠EDF=60，且∠EDF两边分别交边AB，AC于点E，F，那么线段AE，AF，AD之间有怎样的数量关系？并给出证明．
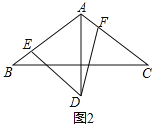
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）
= ； （2）
= ； （3）
；
（4）
； （5）
； （6）a3·a3＝ ；
（7） (x3)5＝ ； （8）(－2x2y3)3＝ ； （9） (x－y)6÷(x－y)3＝ ；
（10）a2b(ab-4b2) （11）（2a-3b）（2a+5b）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com