Question

【题目】如图1，AB为⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE=CB．

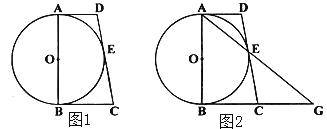
（1）求证：BC为⊙O的切线；

（2）连结AE并延长，交BC的延长线于点G（如图2所示），若AB=2，AD=2，求线段BC和EG的长．

Answer 1

【答案】（1）证明见解析；（2）BC=；EG=．

【解析】

试题分析：（1）连接OE，OC，即可证明△OEC≌△OEC，根据DE与⊙O相切于点E得到OEC=90°，从而证得∠OBC=90°，则BC是圆的切线．

（2）先求线段BC的长，过D作DF⊥BG于F，则四边形ABFD是矩形，有DF=AB=2，在Rt△DCF中，由切线长定理知AD=DE、CE=BC，那么CD=CE+2，CF=CE-2，利用勾股定理可求得CE的长；△ADE中，由于AD=DE，可得到∠DAE=∠AED=∠CEG，而AD∥BG，根据平行线的内错角相等得到∠G=∠EAD=∠CEG，由此可证得CE=CG=CB，即可求得BG的长；在Rt△ABG中，利用勾股定理可求得AG的值，易证△ADE∽△GCE，根据相似三角形的相似比，可求得AE、EG的比例关系，联立AG的长，即可得到EG的值．

试题解析：（1）证明：连接OE，OC；

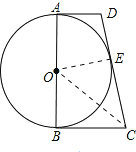
∵CB=CE，OB=OE，OC=OC

∴△OEC≌△OBC（SSS）

∴∠OBC=∠OEC

又∵DE与⊙O相切于点E

∴∠OEC=90°

∴∠OBC=90°

∴BC为⊙O的切线．

（2）解：过点D作DF⊥BC于点F，

∵AD，DC，BG分别切⊙O于点A，E，B

∴DA=DE，CE=CB，

设BC为x，则CF=x-2，DC=x+2，

在Rt△DFC中，（x+2）2-（x-2）2=（2）2，

解得：x=

∵AD∥BG，

∴∠DAE=∠EGC，

∵DA=DE，

∴∠DAE=∠AED；

∵∠AED=∠CEG，

∴∠EGC=∠CEG，

∴CG=CE=CB=，

∴BG=5，

∴AG=；

∵∠DAE=∠EGC，∠AED=∠CEG，

∴△ADE∽△GCE，

∴，

，

解得：EG=．