已知关于x的方程x2+(m+2)x+2m-1=0.
(1)求证:无论m取任何实数,方程总有两个不相等的实数根;
(2)当m为何值时,方程的两根互为相反数?求出此时方程的根.
解:(1)证明:∵a=1,b=m+2,c=2m-1,
∴△=b
2-4ac=(m+2)
2-4×1×(2m-1)=m
2-4m+8=(m-2)
2+4.
∵无论m为任何实数,(m-2)
2≥0,
∴(m-2)
2+4≥4>0.
∴无论m为任何实数,方程总有两个不相等的实数根;
(2)∵方程的解为x=

=
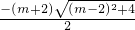
,
∴x
1=
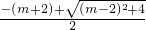
,x
2=

∵方程两根互为相反数,即x
1+x
2=0.
∴
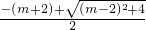
+

=0,
∴
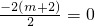
.
∴m=-2.即当m=-2时,方程的两根互为相反数.
把m=-2代入方程x
2+(m+2)x+2m-1=0,
解得x=±

,
当方程的两根互为相反数时,此时方程的根为x
1=

,x
2=-

.
分析:(1)根据题意求出△的值,判断出△的符号即可;
(2)先根据求根公式求出x的值,再根据两根互为相反数即可求出m的值,把m的值代入原方程求出x的值即可.
点评:本题考查的是根与系数的关系,熟知一元二次方程ax
2+bx+c=0(a≠0)的根与△=b
2-4ac的关系是解答此题的关键.

 =
=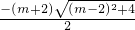 ,
,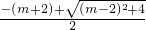 ,x2=
,x2=
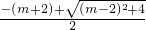 +
+ =0,
=0,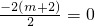 .
. ,
, ,x2=-
,x2=- .
.
