
 ,半径为1,C为劣弧
,半径为1,C为劣弧 的中点,试判定四边形OACB的形状,并说明理由.
的中点,试判定四边形OACB的形状,并说明理由.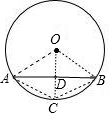 解:如图,连OA,OB,AC,BC,OC,OC与AB交于点D,
解:如图,连OA,OB,AC,BC,OC,OC与AB交于点D, 的中点,
的中点, ,OA=1,
,OA=1, ,DO=
,DO= ,而OC=1,
,而OC=1, 的中点,根据垂径定理的推论得到OC⊥AB,AD=BD,而AB=
的中点,根据垂径定理的推论得到OC⊥AB,AD=BD,而AB= ,OA=1,根据勾股定理得到DO=
,OA=1,根据勾股定理得到DO= ,即D为OC的中点,OC和AB相互垂直平分,根据菱形的判定方法即可得到四边形OACB的形状.
,即D为OC的中点,OC和AB相互垂直平分,根据菱形的判定方法即可得到四边形OACB的形状.

科目:初中数学 来源: 题型:
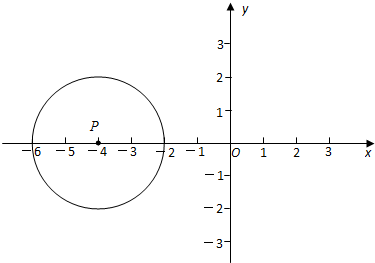
 M与x轴没有交点,且圆心M在第一象限内,P是x轴正半轴上一动点,MQ⊥AB于Q,且MP=3cm,设OA=ycm,OP=xcm.
M与x轴没有交点,且圆心M在第一象限内,P是x轴正半轴上一动点,MQ⊥AB于Q,且MP=3cm,设OA=ycm,OP=xcm.查看答案和解析>>
科目:初中数学 来源: 题型:
 | AB |
查看答案和解析>>
科目:初中数学 来源: 题型:

 |
| BC |
| PA-PB |
| PD |


查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广东卷)数学 题型:解答题
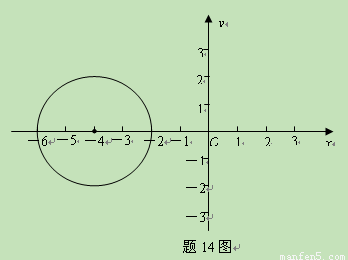
如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿x轴向右平移4个单位长度得⊙P1.
(1)画出⊙P1,并直接判断⊙P与⊙P1的位置关系;
(2)设⊙P1与x轴正半轴,y轴正半轴的交点分别为A,B,求劣弧AB与弦AB围成的图形的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com