
【题目】如图,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=4,OC=10,∠A=60°,线段EF垂直平分OD,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E'关于x轴对称,连接BP、E'M,则BP+PM+ME'的长度的最小值为______.

【答案】![]()
【解析】
连接OP,先确定OD的长和B点坐标,然后证明四边形OPME'是平行四边形,可得OP=EM,因为PM是定值,推出PB+ME'=OP+PB的值最小时,即当O、P、B共线时BP+PM+M E的长度最小,最后根据两点间的距离公式和线段的和差解答即可.
解:如图:连接OP

在Rt△ADO中,∠A=60°,AD=4,
∴OD=4tan60°=4![]() ,
,
∴A(-4,4![]() )
)
∵四边形ABCD是平行四边形,
∴AB=OC=10,
∴DB=10-4=6
∴B(6,4![]() )
)
∵线段EF垂直平分OD
∴OE=![]() OD=2
OD=2![]() ,∠PEO=∠EOM=∠PM0=90°,
,∠PEO=∠EOM=∠PM0=90°,
∴四边形OMPE是矩形,
∴PM=OE=2![]() ,
,
∵OE=0E'
∴PM=OE',PM//OE',
∴四边形OPME'是平行四边形,
∴0P=EM,
∵PM=2![]() 是定值,
是定值,
∴PB+ME'=OP+PB的值最小时,BP+PM+ME的长度最小,
∴当0、P、B共线时,BP+PM+ME的长度最小
∴BP+PM+ME的最小值为OB+PM=![]() .
.
故答案为![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度![]() 与甲盒数量
与甲盒数量![]() 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨 | 频数 | 频率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合计 | d | 1.00 |

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的点(不与点B,C重合),连结AD

(1)如图1,当点D是BC边上的中点时,则S△ABD:S△ACD=_________(直接写出答案)
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,S△ABD:S△ACD=_________ (用含m,n的代数式表示).
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连结BE,如果AC=2,AB=4,S△BDE =6,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
已知:如图,∠D=110°,∠EFD=70°,∠1=∠2,
求证:∠3=∠B

证明:∵∠D=110°, ∠EFD=70°(已知)
∴∠D+∠EFD=180°
∴AD∥______( )
又∵∠1=∠2(已知)
∴_____∥BC ( 内错角相等,两直线平行)
∴EF∥_____ ( )
∴∠3=∠B(两直线平行,同位角相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
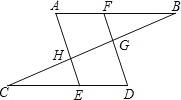
【题目】已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC与H,G,∠A=∠D,∠FGB+∠EHG=180°.
(1)求证:AB∥CD;
(2)若AE⊥BC,直接写出图中所有与∠C互余的角,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象交于点A(﹣2,﹣5),C(5,n),交y轴于点B,交x轴于点D.
的图象交于点A(﹣2,﹣5),C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数![]() 和一次函数y1=kx+b的表达式;
和一次函数y1=kx+b的表达式;
(2)连接OA,OC,求△AOC的面积;
(3)根据图象,直接写出y1>y2时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于![]() 、
、![]() 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转![]() 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.

(1)求证,![]() ;
;
(2)如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;

(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2, ![]() ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1, ![]() ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com