
【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于![]() 、
、![]() 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转![]() 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.

(1)求证,![]() ;
;
(2)如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;

(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
【答案】(1)![]() ,见解析;(2)D(3,1),
,见解析;(2)D(3,1),![]() 平移的距离是
平移的距离是![]() 个单位,见解析;(3)存在满足条件的点Q,其坐标为
个单位,见解析;(3)存在满足条件的点Q,其坐标为![]() 或
或![]() 或
或![]() ,见解析.
,见解析.
【解析】
(1)根据AAS或ASA即可证明;
(2)首先求直线AB的解析式,再求出出点D的坐标,再求出直线B′C′的解析式,求出点C′的坐标即可解决问题;
(3)如图3中,作CP∥AB交y轴于P,作PQ∥CD交AB于Q,则四边形PCDQ是平行四边形,求出直线PC的解析式,可得点P坐标,点C向左平移1个单位,向上平移![]() 个单位得到P,推出点D向左平移1个单位,向上平移
个单位得到P,推出点D向左平移1个单位,向上平移![]() 个单位得到Q,再根据对称性可得Q′、Q″的坐标.
个单位得到Q,再根据对称性可得Q′、Q″的坐标.
(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
(2)∵直线AB与x轴,y轴交于![]() 、
、![]() 两点
两点
∴直线AB的解析式为![]()
∵![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]()
把![]() 代入
代入![]() 得到
得到![]() ,
,
∴![]()
∵![]() ,
,![]()
∴直线BC的解析式为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() 代入得到
代入得到![]()
∴直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 平移的距离是
平移的距离是![]() 个单位.
个单位.
(3)如图3中,作CP∥AB交y轴于P,作PQ∥CD交AB于Q,则四边形PCDQ是平行四边形,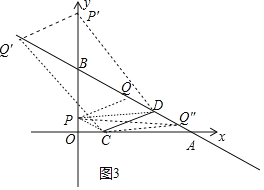
易知直线PC的解析式为y=-![]() x+
x+![]() ,
,
∴P(0,![]() ),
),
∵点C向左平移1个单位,向上平移![]() 个单位得到P,
个单位得到P,
∴点D向左平移1个单位,向上平移![]() 个单位得到Q,
个单位得到Q,
∴Q(2,![]() ),
),
当CD为对角线时,四边形PCQ″D是平行四边形,可得Q″![]() ,
,
当四边形CDP′Q′为平行四边形时,可得Q′![]() ,
,
综上所述, 存在满足条件的点Q,其坐标为![]() 或
或![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图:在![]() 中,已知AB=AC,垂足为点D,点F在AD的延长线上,且CE∥BF,试说明DE=DF的理由.
中,已知AB=AC,垂足为点D,点F在AD的延长线上,且CE∥BF,试说明DE=DF的理由.

解:因为AB=AC,AD⊥BC(已知)
所以BD=
因为CE∥BF(已知)
所以![]() =
=
在![]() 中,
中,
![]() 中
中
=
=
所以![]() ( )
( )
所以DE=DF( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=4,OC=10,∠A=60°,线段EF垂直平分OD,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E'关于x轴对称,连接BP、E'M,则BP+PM+ME'的长度的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂生产三种不同型号的电视机,出厂价分别为甲种每台1500元, 乙种每台2100元, 丙种每台2500元, 若商场同时购进其中两种不同型号的电视机共50台,用去9万元.请你通过计算,说明商场有哪些进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇道路改造工程,由甲、乙两工程队合作完成.甲工程队单独施工比乙工程队单独施工多用30天完成此项工程,甲工程队30天完成的工程与甲、乙两工程队10天完成的工程相等.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,才能使施工费不超过64万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于_______海里.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com