Question

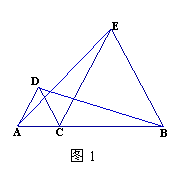
（1）如图1，在线段AB上取一点C（BC>AC），分别以AC、BC为边在同一侧作等边ACD与等边BCE，连结AE、BD，则ACE经过怎样的变换（平移、轴对称、旋转）能得到DCB？请写出具体的变换过程；（不必写理由）

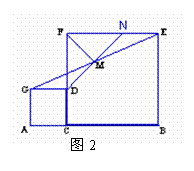
（2）如图2，在线段AB上取一点C（BC>AC），如果以AC、BC为边在同一侧作正方形ACDG与正方形CBEF，连结EG，取EG的中点M，设 DM的延长线交EF于N，并且DG=NE;请探究DM与FM的关系，并加以证明；

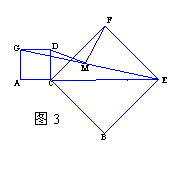
（3）在图2的基础上，将正方形CBEF绕点C顺时针旋转（如图3），使得A、C、E在同一条直线上，请你继续探究线段MD、MF的关系，并加以证明.

 

Answer 1

（1）将ACE绕点C顺时针旋转60°后能得到DCB

(2) 如图（2），答：相等且垂直．

先证MGD≌MEN

∴DM=NM．在中，．

∵NE=GD, GD=CD，∴NE=CD，∴FN=FD

即FM⊥DM，

∴DM与 FM相等且垂直

(3)如图（3），答：相等且垂直．延长DM交CE于N，连结DF、FN

先证MGD≌MNE

∴DM =NM, NE=DG．

∵∠DCF=∠FEN=45°，DC=DG=NE，FC=FE，　　　　　　　　∴DCF≌NEF，∴DF=FN, ∠DFC=∠NFE，               

可证∠DFN=90°，

即FM=DM, FM⊥DM

∴DM与 FM相等且垂直