

| nπr |
| 180 |
| nπ(r+6) |
| 180 |
| r |
| r+6 |
| 2 |
| 3 |

| nπ12 |
| 180 |
| 3 |



科目:初中数学 来源:学习周报 数学 北师大九年级版 2009-2010学年 第10期 总第166期 北师大版 题型:044
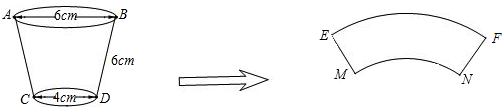
某班课题学习小组,进行一次路灯下的问题探究.其结果是:
a.测量出如图中的一组数据,并算出了路灯距离地面的高度;

b.提出了一个问题:
问题:如果小明从路灯的正下方P开始,向远处作匀速直线运动,那么他头顶的影子在地面上作的也是匀速直线运动吗?(如图).

根据上述情景和问题完成下列任务:
(1)如图1所示,请你算一算路灯距离地面的高度;
(2)对于问题你会怎样猜想?若你也是课题组中的一员,请你设计一个操作方案验证你的猜想,并用我们所学的几何知识给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题




查看答案和解析>>
科目:初中数学 来源:2010年江苏省无锡市惠山区八校联考中考适应性训练数学试卷(解析版) 题型:解答题




查看答案和解析>>
科目:初中数学 来源:2011年江西省师大附中和南大附中七校联考数学试卷(解析版) 题型:解答题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com