
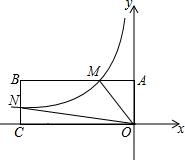
 如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4).
如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4). 分析 先利用B点坐标得到S矩形ABCO=6,M点的纵坐标为1,再利用反比例函数解析式可确定M(-2,1),接着根据反比例函数的比例系数k的几何意义得到S△ONC=S△OAM=1,则S四边形OMBN=4,设P(0,t),则S△OMP=$\frac{1}{2}$×2×|t|=4,然后解方程求出t即可得到P点坐标.
解答 解:∵顶点B的坐标为(-6,1).
∴BC=1,OC=6,
∴S矩形ABCO=6,
∵反比例函数y=-$\frac{2}{x}$(x<0)的图象过点M、N,
当y=1时,-$\frac{2}{x}$=1,解得x=-2,则M(-2,1),
∴S△ONC=S△OAM=$\frac{1}{2}$×|-2|=1,
∴S四边形OMBN=6-1-1=4,
设P(0,t),
∴S△OMP=$\frac{1}{2}$×2×|t|=4,解得t=4或t=-4,
∴P点坐标为(0,4)或(0,-4).
故答案为(0,4)或(0,-4).
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.


科目:初中数学 来源: 题型:选择题
| 年龄(单位:岁) | 12 | 13 | 14 | 15 |
| 人数 | 4 | 3 | 2 | 1 |
| A. | 12,13.1 | B. | 12,13 | C. | 13,13.1 | D. | 13,13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
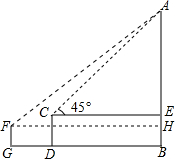 在数学活动课上,小明和小红分别在不同位置测量学校的旗杆高度,如图是他们在测量后绘制的示意图,小明测角仪测得旗杆顶端A的仰角∠ACE=45°,测角仪的高度CD=1.7m,测角仪CD的底部D处与旗杆的底部B处之间的距离DB=8.6cm,小红用同样的方法测得数据∠AFH=40°,FG=1.5cm,GB=10.2cm,点G,D,B在同一条直线上.
在数学活动课上,小明和小红分别在不同位置测量学校的旗杆高度,如图是他们在测量后绘制的示意图,小明测角仪测得旗杆顶端A的仰角∠ACE=45°,测角仪的高度CD=1.7m,测角仪CD的底部D处与旗杆的底部B处之间的距离DB=8.6cm,小红用同样的方法测得数据∠AFH=40°,FG=1.5cm,GB=10.2cm,点G,D,B在同一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
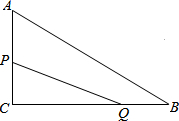 如图,在Rt△ACB中,∠C=90°,AC=6cm,CB=8cm,点P、Q同时由A,B两点出发分别沿AC、BC方向向点C匀速移动,它们的速度都是1cm/s,几秒后△PCQ的面积和四边形APQB的面积相等?
如图,在Rt△ACB中,∠C=90°,AC=6cm,CB=8cm,点P、Q同时由A,B两点出发分别沿AC、BC方向向点C匀速移动,它们的速度都是1cm/s,几秒后△PCQ的面积和四边形APQB的面积相等?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
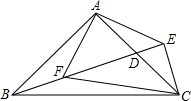 已知如图,Rt△ABC中,∠BAC=90°,AB=AC,D是AC的中点,过C作CE⊥BD交BD的延长线于E,连结AE,过A作AF⊥AE交BD于F.
已知如图,Rt△ABC中,∠BAC=90°,AB=AC,D是AC的中点,过C作CE⊥BD交BD的延长线于E,连结AE,过A作AF⊥AE交BD于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25° | B. | 65° | C. | 115° | D. | 155° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com