
 ��ͼ��������y=-
��ͼ��������y=-| 1 | 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |
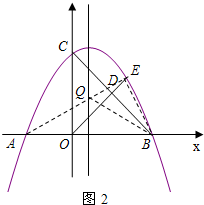 ��QA=QB��
��QA=QB��| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG|
26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG|�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
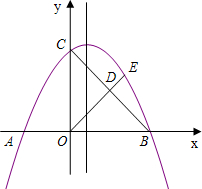
 ��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4����
��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
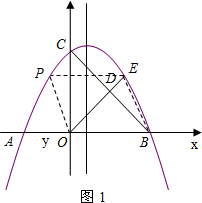
 ��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮
����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������
��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������| A��-1��x��3 | B��3��x��-1 | C��x��-1��x��3 | D��x��-1��x��3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com