(1)证明:∵AB∥CD,
∴∠ABC=∠DCB,
∵EC=BF,
∴EC+BC=BF+BC,
∴EB=CF,
∵在△ABE和△DCF中
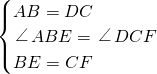
∴△ABE≌△DCF(SAS).
∴∠A=∠D.
(2)解:∵AD∥BC,∠A=90°,
∴∠ABC=90°,
∵,∠ABD=15°,
∴∠DBC=75°,
又∵∠C=60°,
∴∠BDC=45°.

过D作DE⊥BC于E,过B作BF⊥DC于F,
∵∠C=60°,
∴∠FBC=30°,
∴CF=

BC=

×2=1,
∵∠DBC=75°,
∴∠DBF=45°,
∴∠BDF=45°=∠DBF,
∴BF=DF,
在Rt△BFC中,由勾股定理得:BF=

=

,
∴DF=

,DC=1+

,
在△DBC中,由三角形的面积公式得:

BC×DE=

DC×BF,

×2×DE=

×(1+

)×

,
DE=
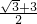
,
∵∠ABC=90°,DE⊥BC,
∴AB∥DE,
∵AD∥BC,
∴四边形ABED是平行四边形,
∴AB=DE=
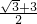
.
分析:(1)求出BE=CF,∠ABC=∠DCF,根据SAS证出△ABE≌△DCF即可;
(2)求出∠DBC,根据三角形内角和定理求出∠BDC即可;过D作DE⊥BC于E,过B作BF⊥DC于F,求出CF、BF、DF,根据三角形面积公式求出DE,即可求出答案.
点评:本题考查了平行四边形性质,全等三角形的性质和判定,平行线性质,三角形的面积公式,解直角三角形等知识点的应用,主要考查学生综合运用性质进行推理的能力.


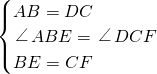

 BC=
BC= ×2=1,
×2=1, =
= ,
, ,DC=1+
,DC=1+ ,
, BC×DE=
BC×DE= DC×BF,
DC×BF, ×2×DE=
×2×DE= ×(1+
×(1+ )×
)× ,
,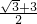 ,
,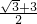 .
.

 阅读快车系列答案
阅读快车系列答案 如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.
如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.