(1)解:∵AB是⊙O直径,
∴∠ACB=90°,
故答案为:90°;
(2)证明:∵OD⊥BC,
∴∠OEB=90°,
∵∠ACB=90°,
∴∠OEB=∠ACB,
∴OE∥AC;
(3)解:
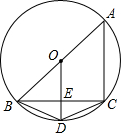
∵OD⊥BC,OD是⊙O半径,BE=4,
∴BC=2BE=8,
在Rt△BCA中,∠C=90°,BC=8,AC=6,由勾股定理得:AB=10,
即OB=OD=5,
在Rt△OBE中,由勾股定理得:OB
2=OE
2+BE
2,
即5
2=(5-DE)
2+4
2,
解得:DE=2.
分析:(1)根据直径所对的圆周角是直角得出即可;
(2)根据垂直得出∠OEB=∠ACB=90°,根据平行线的判定推出即可;
(3)根据垂径定理求出BC,根据勾股定理求出AB,得出OD和OB,在△OBE中,根据勾股定理即可求出DE.
点评:本题考查了垂径定理,勾股定理,圆周角定理,平行线的判定等知识点,能正确运用这些定理进行推理是解此题的关键.

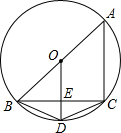 如图,圆内接四边形ABCD,AB是⊙O的直径,OD⊥BC于E.
如图,圆内接四边形ABCD,AB是⊙O的直径,OD⊥BC于E. ∵OD⊥BC,OD是⊙O半径,BE=4,
∵OD⊥BC,OD是⊙O半径,BE=4,
