练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列命题中，真命题是（　　）

    　

    A．

    两条对角线垂直且相等的四边形是正方形

    　

    B．

    两条对角线互相垂直的四边形是菱形

    　

    C．

    两条对角线互相平分且相等的四边形是矩形

    　

    D．

    同一底上两个角相等的四边形是等腰梯形


    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图3所示，有一张一个角为60°的直角三角形纸片，沿其一条中位线剪开后，    

       不能拼成的四边形是（    )                                       

       A、邻边不等的矩形      B、正方形      C、有一角是锐角的菱形      等腰梯

    查看答案和解析>>

    科目：初中数学 来源： 题型：


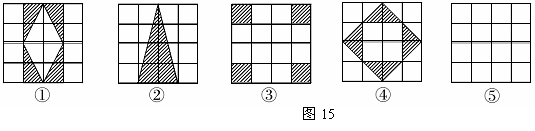
    （1）观察图15①～④中阴影部分构成的图案，请写出这四个图案都具有的两个共同特征；

    　 （2）借助图15⑤的网格，请设计一个新的图案，使该图案同时具有你在解答（1）中所写出的两个共同特征．（注意：新图案与图14①～④的图案不能重合）


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图两个同心圆中，四条直径把大圆分成八等份，若往圆面投掷飞镖，则飞镖落在黑色区域的概率是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一组数据：10、5、15、5、20，则这组数据的平均数和中位数分别是（　　）

    　

    A．

    10，10

    B．

    10，12.5

    C．

    11，12.5

    D．

    11，10

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点（﹣6，y1），（8，y2）都在直线y=﹣x﹣6上，则y1，y2大小关系是（　　）

    　

    A．

    y1＞y2

    B．

    y1=y2

    C．

    y1＜y2

    D．

    不能比较

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在菱形ABCD中，AB=13cm，BC边上的高AH=5cm，那么对角线AC的长为　_________　cm．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点（-4，），（2，）都在直线上，则，大小关系是（  ）

    A、＞          B、=       C、＜    D、不能比较

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读下列材料：

    某同学遇到这样一个问题：如图1，在△ABC中，AB=AC，BD是△ABC的高．P是BC边上一点，PM，PN分别与直线AB，AC垂直，垂足分别为点M，N．求证：．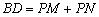

    他发现，连接AP，有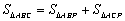，即．由AB=AC，可得．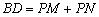

    他又画出了当点P在CB的延长线上，且上面问题中其他条件不变时的图形，如图2所示．他猜想此时BD，PM，PN之间的数量关系是：．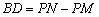

    请回答：

    （1）请补全以下该同学证明猜想的过程；

    证明：连接AP．

    ∵         ，

    ∴              ．

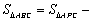    ∵AB=AC，

    ∴．

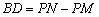    （2）参考该同学思考问题的方法，解决下列问题：

    在△ABC中，AB=AC=BC，BD是△ABC的高．P是△ABC所在平面上一点，PM，PN，PQ分别与直线AB，AC，BC垂直，垂足分别为点M，N，Q．

    ①如图3，若点P在△ABC 的内部，则BD，PM，PN，PQ之间的数量关系是：                           ；

    ②若点P在如图4所示的位置，利用图4探究得出此时BD，PM，PN，PQ之间的数量关系是：                           ．

    查看答案和解析>>

    同步练习册答案