
分析 将点(2,0)、(1,-1)代入二次函数的解析式,利用待定系数法法求该二次函数的解析式即可.
解答 解:根据题意,得$\left\{\begin{array}{l}{4a+2b=0}\\{a+b=-1}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$;
∴该二次函数的解析式为:y=x2-2x,开口向上.
点评 本题主要考查了待定系数法求二次函数的解析式.解题时,借用了二次函数图象上点的坐标特征:经过图象上的点一定在函数图象上,且图象上的每一个点均满足该函数的解析式.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
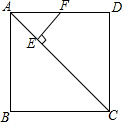 如图,正方形ABCD的边长为1,AC为其对角线,点E为AC上一点且满足CE=CD,过点E作EF⊥AC交AD于点F,则DF的长度为$\sqrt{2}$-1.
如图,正方形ABCD的边长为1,AC为其对角线,点E为AC上一点且满足CE=CD,过点E作EF⊥AC交AD于点F,则DF的长度为$\sqrt{2}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任何数都不等于它的相反数 | |
| B. | 若|x|=2,那么x一定是2 | |
| C. | 有比-1大的负整数 | |
| D. | 如果a>b>1,那么a的倒数小于b的倒数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
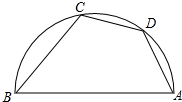 如图,AB是⊙O的直径,点D是弧$\widehat{AC}$的中点,∠ABC=52°,则∠DAB等于( )
如图,AB是⊙O的直径,点D是弧$\widehat{AC}$的中点,∠ABC=52°,则∠DAB等于( )| A. | 58° | B. | 61° | C. | 72° | D. | 64° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com