
【题目】计算(1)(x+y)2﹣(x﹣y)2
(2)![]()
(3)(2x-y+3)(2x+y-3)
(4)(2m+3n)2(2m-3n)2
【答案】(1)4xy;
(2)-4;
(3)![]() ;
;
(4)![]() .
.
【解析】
(1)先运用完全平方式展开,然后合并同类项即可;
(2)先计算同底数幂的除法,再计算加法运算即可;
(3)先运用平方差公式计算,然后再运用完全平方式展开,最后去括号即可;
(4)先运用平方差公式计算,然后再运用完全平方式展开即可.
解:(1)(x+y)2﹣(x﹣y)2
=x2+2xy+y2-x2+2xy-y2
=4xy;
(2)![]()
=1+(-5)3-2
=1-5
=-4;
(3)(2x-y+3)(2x+y-3)
=(2x)2-(y-3)2
=4x2-(y2-6y+9)
=4x2-y2+6y-9;
(4)(2m+3n)2(2m-3n)2
=(4m2-9n2)2
=16m4-72m2n2+81n4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人再次选择自行车作为出行工具,小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题: 
(1)a= , b= , m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是v米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.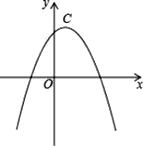
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( ) 
A.6cm
B.7cm
C.8cm
D.9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x、y的二元一次方程组![]() 的解都为正数.
的解都为正数.
(1)求a的取值范围;
(2)化简|a+1|﹣|a﹣1|;
(3)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一种圆环甲(如图1),它的外圆直径是8厘米,环宽1厘米。
①如果把这样的2个圆环扣在一起并拉紧(如图2),长度为 厘米;
②如果用n个这样的圆环相扣并拉紧,长度为 厘米。
(2)另一种圆环乙,像(1)中圆环甲那样相扣并拉紧,
①3个圆环乙的长度是28cm,5个圆环乙的长度是44cm,求出圆环乙的外圆直径和环宽;
②现有n(n>2)个圆环甲和n(n>2)个圆环乙,将它们像(1)中那样相扣并拉紧,长度用n的代数式表示为多少厘米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为____________,△ADF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() 与
与 ![]() 轴、
轴、 ![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与 ![]() 轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com