
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为____________,△ADF是等腰三角形.

【答案】40°或20°.
【解析】
根据旋转的性质得∠DCA=α,CD=CA,则∠CDA=∠CAD=![]() (180°α)=90°
(180°α)=90°![]() α,利用三角形外角的性质得∠DFA=30°+α,当△ADF是等腰三角形,若FD=FA,则∠FDA=∠FAD,不合题意;然后讨论AF=AD或DF=DA,分别利用等腰三角形的性质得到90°
α,利用三角形外角的性质得∠DFA=30°+α,当△ADF是等腰三角形,若FD=FA,则∠FDA=∠FAD,不合题意;然后讨论AF=AD或DF=DA,分别利用等腰三角形的性质得到90°![]() α=30°+α;30°+α=90°
α=30°+α;30°+α=90°![]() α30°,即可得到α的值.
α30°,即可得到α的值.
解:∵△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,
∴∠DCA=α,CD=CA,
∴∠CDA=∠CAD=![]() (180°α)=90°
(180°α)=90°![]() α,
α,
∵△ADF是等腰三角形,∠DFA=30°+α,
①当FD=FA,则∠FDA=∠FAD,不合题意,舍去;
②当AF=AD,则∠ADF=∠AFD,
∴90°![]() α=30°+α,
α=30°+α,
解得α=40°;
③当DF=DA,则∠DFA=∠DAF,
∴30°+α=90°![]() α30°,
α30°,
解得α=20°,
故答案为40°或20°.


科目:初中数学 来源: 题型:
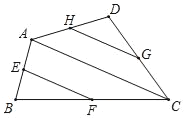
【题目】如图,点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点.
(1)如果图中线段都可画成有向线段,那么在这些有向线段所表示的向量中,与向量![]() 相等的向量是 ;
相等的向量是 ;
(2)设![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .试用向量
.试用向量![]() ,
,![]() 或
或![]() 表示下列向量:
表示下列向量:![]() = ;
= ;![]() = .
= .
(3)求作:![]()
![]() .(请在原图上作图,不要求写作法,但要写出结论)
.(请在原图上作图,不要求写作法,但要写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,某车行经营的A型车去年2月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年2月份与去年2月份卖出的A型车数量相同,则今年2月份A型车销售总额将比去年2月份销售总额增加25%.
(1)求今年2月份A型车每辆销售价多少元?
(2)该车行计划今年3月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的2倍,A.B两种型号车的进货和销售价格如表,问应如何进货才能使这批车获利最多?
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段a,b,c,用直尺和圆规画图(保留画图痕迹,并用字母表示出所画的线段).
![]()
(1)画一条线段,使它等于a+b;(2)画一条线段,使它等于a-c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
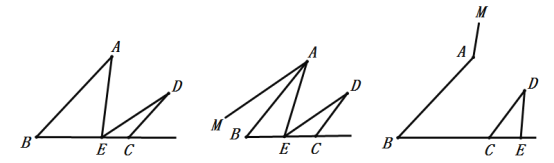
【题目】点D在∠ABC内,点E为边BC上一点,连接DE、CD.
(1)如图1,连接AE,若∠AED=∠A+∠D,求证:AB//CD.
(2)在(1)的结论下,过点A的直线MA//ED.
①如图2,当点E在线段BC上时,猜想并验证∠MAB与∠CDE的数量关系;
②如图3,当点E在线段BC的延长线上时,猜想并验证∠MAB与∠CDE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体考在即,初三(1)班的课题研究小组对本年级530名学生的体育达标情况进行调查,制作出如图所示的统计图,其中1班有50人.(注:30分以上为达标,满分50分)根据统计图,解答下面问题:
(1)初三(1)班学生体育达标率和本年级其余各班学生体育达标率各是多少?
(2)若除初三(1)班外其余班级学生体育考试成绩在30﹣﹣40分的有120人,请补全扇形统计图;(注:请在图中分数段所对应的圆心角的度数)
(3)如果要求全年级学生的体育达标率不低于90%,试问在本次调查中,该年级全体学生的体育达标率是否符合要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com