
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
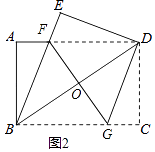
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
【答案】
(1)
证明:如图1,根据折叠,∠DBC=∠DBE,
又AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF,
∴△BDF是等腰三角形;
(2)
解:①∵四边形ABCD是矩形,
∴AD∥BC,
∴FD∥BG,
又∵FD∥BG,
∴四边形BFDG是平行四边形,
∵DF=BF,
∴四边形BFDG是菱形;
②∵AB=6,AD=8,
∴BD=10.
∴OB= ![]() BD=5.
BD=5.
假设DF=BF=x,∴AF=AD﹣DF=8﹣x.
∴在直角△ABF中,AB2+A2=BF2,即62+(8﹣x)2=x2,
解得x= ![]() ,
,
即BF= ![]() ,
,
∴FO= ![]() =
= ![]() =
= ![]() ,
,
∴FG=2FO= ![]() .
.
【解析】(1)根据两直线平行内错角相等及折叠特性判断;(2)①根据已知矩形性质及第一问证得邻边相等判断;②根据折叠特性设未知边,构造勾股定理列方程求解.
【考点精析】根据题目的已知条件,利用平行线的性质和矩形的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.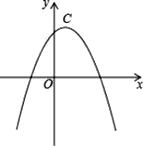
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为____________,△ADF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
A.3m
B.![]() m
m
C.![]() m
m
D.4m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() 与
与 ![]() 轴、
轴、 ![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与 ![]() 轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.
妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com